Abstrakt
Skúmali sme použiteľnosť modifikovanej metódy skúšky medzivrstvového šmyku vrubovým tlakom, ktorá je účinná na získanie medzivrstvových šmykových vlastností termoplastických CFRP, na hladké tkané materiály GFRP, ktoré sa široko používajú v priemysle. Na základe výsledkov pozorovania mezoskalárnej štruktúry pomocou röntgenového CT sa vytvoril model analýzy CAE a vykonala sa homogenizačná analýza so zameraním na obmedzujúce podmienky skúšobnej vzorky z hľadiska koeficientu trenia. Namerané hodnoty a výsledky analýzy vykazovali dobrú zhodu.
Úvod
V posledných rokoch sa plasty vystužené sklenenými vláknami (GFRP), ktoré majú vysokú špecifickú pevnosť a vynikajúcu spracovateľnosť a tvarovateľnosť, vo veľkej miere používajú na elektronické substráty, lode a vonkajšie časti automobilov a stali sa nepostrádateľným materiálom. GFRP, ktorý je kompozitným materiálom, má anizotropiu a vykazuje komplikované deformačné a lomové správanie v závislosti od smeru hlavnej osi pôsobiaceho napätia: ťah, tlak, ohyb, šmyk v rovine, medzilamelový a mimorovinový šmyk alebo ich kombinácia. Pri navrhovaní výrobkov pomocou počítačom podporovaného inžinierstva (CAE) je veľmi potrebné používať skúšobné metódy, ktoré dokážu vyhodnotiť správanie sa pri poruche každého komponentu jednotlivo.
*1 Cybernet Systems Co., Ltd. Mechanical CAE Div.
*2 SHIMADZU CORPORATION
Nehorľavý typ 4 (FR4), ktorý je vyrobený zo sklenených vlákien a epoxidovej živice, sa široko používa v doskách s plošnými spojmi pre elektronické zariadenia.
Dôvodom intenzívneho používania FR4 je skutočnosť, že hladko tkaný materiál GFRP má vysoké elektroizolačné vlastnosti a nehorľavosť a že v dôsledku tepla dochádza len k malým rozmerovým zmenám povrchu v dôsledku spevňujúceho účinku sklených vlákien. Keďže však tento materiál má vrstvenú štruktúru, vlákna sú orientované v rovine, ale medzi laminami nie je takmer žiadna orientácia vlákien, čo z neho robí štruktúru bohatú na živicu. Preto, zatiaľ čo v smere do roviny sa prejavujú vynikajúce mechanické vlastnosti, výstužný účinok vlákien je v medzilaminárnom smere slabý, takže prevládajú fyzikálne vlastnosti matricovej živice a očakáva sa nelineárne správanie v dôsledku poddajnosti živice. Je dôležité presne pochopiť medzilamelové šmykové vlastnosti, aby bolo možné pomocou numerickej simulácie reprodukovať deformačné správanie, ktoré je výrazne ovplyvnené vlastnosťami matricovej živice, napríklad ohyb a odlupovanie.
Ako reprezentatívne metódy merania medzilamelových šmykových vlastností kompozitov bolo navrhnutých niekoľko skúšobných metód (1-3). Pri každej skúšobnej metóde je tvar prípravku komplikovaný a je ťažké vyrobiť skúšobnú vzorku na skúšku medzilamelového šmyku, pretože veľkosť skúšobnej vzorky musí byť dlhá vzhľadom na smer laminovania kompozitného materiálu
(4). Mimochodom, metóda skúšky pevnosti v medziplášťovom strihu vrubovým stlačením, pri ktorej sa na čelnú stranu malej skúšobnej vzorky pôsobí tlakovým zaťažením a ktorá je uvedená v norme JIS K 7092, sa široko používa ako skúšobná metóda, ktorou možno ľahko vyhodnotiť pevnosť v medziplášťovom strihu plastov vystužených uhlíkovými vláknami (CFRP).
(5). Veľkosť skúšobnej vzorky v smere laminovania potrebná na túto skúšku je len 3,5 až 6,5 mm, čo umožňuje jednoduchú výrobu skúšobných vzoriek s malým množstvom materiálu. Touto skúšobnou metódou však nie je možné získať šmykovú deformáciu, pretože oblasť, v ktorej sa sústreďuje medzilamelová šmyková deformácia, je veľmi úzka.
Pokiaľ však ide o metódu tlakovej skúšky termosetových CFRP, v predchádzajúcom výskume
(6) výpočtom sa navrhlo, že oblasť medzilamelového šmykového namáhania sa môže rozšíriť zvýšením veľkosti prekrytia drážok zárezu. V posledných rokoch boli publikované príklady modifikovaných tlakových medzilamelových strihových skúšok so zárezmi, pri ktorých sa oblasť medzilamelovej strihovej deformácie môže rozšíriť prehĺbením zárezovej drážky skúšobnej vzorky a do oblasti deformácie sa môže pripojiť tenzometer
(4). Zistilo sa, že nelineárne charakteristiky medzilamelového šmyku možno získať priamo z vypočítaného nominálneho šmykového napätia získaného vydelením tlakovej skúšobnej sily získanej zo skúšobného stroja šmykovou plochou medzi vrubovými drážkami a nameranej deformácie získanej z tenzometra. Pri tejto skúšobnej metóde sa na pozorovanie a vyhodnotenie malých plôch použila digitálna kamera synchronizovaná so skúšobným strojom a meranie deformácie sa vykonalo pomocou analýzy digitálnej obrazovej korelácie (DIC). Použitím DIC analýzy na meranie deformácie sa zistilo, že medzilamelovú šmykovú deformáciu možno ľahko merať od malej deformácie až po veľkú deformáciu bez obáv z vypadnutia alebo limitov merania počas merania tenzometrom. V tomto článku skúmame, či je modifikovaná metóda skúšky vrubovým tlakom, ktorá je účinná pri získavaní medzilamelových šmykových vlastností termoplastického CFRP, použiteľná na hladký tkaný GFRP, ktorý je materiálom vystuženým nekonečnými vláknami široko používaným v priemysle.
Na druhej strane, úsilie nahradiť časť skutočných testov numerickou simuláciou (CAE analýza) je čoraz dôležitejšie v reakcii na zníženie rôznych nákladov spojených s výrobou prototypov a nedávne hnutie na podporu digitálnej transformácie (7) spojené s problémom nových koronavírusov. Vstupné informácie potrebné na dosiahnutie analýzy CAE možno vo všeobecnosti rozdeliť na tri typy: modely analýzy, vlastnosti materiálov a okrajové podmienky. Najmä v prípade kompozitných materiálov s anizotropiou je veľmi ťažké získať materiálové vlastnosti. Pružné správanie izotropných materiálov je charakterizované štyrmi vlastnosťami: Youngovým modulom, Poissonovým pomerom, modulom v šmyku a objemovým modulom. Vo všeobecnosti sa ako vstupné hodnoty používajú Youngov modul a Poissonov pomer, ktoré sa experimentálne ľahko merajú, a meranie šmykového modulu sa nevyžaduje. V prípade anizotropných materiálov sú však Youngov modul a modul v šmyku navzájom nezávislé a musia sa merať nezávisle.
Súbežne so snahami o získanie vyššie opísaného modulu pružnosti v šmyku testovaním sa uskutočnilo mnoho štúdií zameraných na analytické predpovedanie vlastností materiálu.
Pravidlo miešania (8), ktoré je známe ako najklasickejšia metóda, umožňuje predpovedať vlastnosti materiálu pomocou jednoduchých výpočtov, ktoré možno vykonať ručne. Pravidlo miešania však predpokladá, že vlákna a živice, ktoré tvoria kompozit, sú zapojené sériovo alebo paralelne so smerom osi zaťaženia, alebo inými slovami, na uľahčenie výpočtu sa predpokladajú idealizované podmienky, takže ho možno použiť len na veľmi obmedzené kompozitné materiály, ako je napríklad jednosmerná výstuž. Metóda ekvivalentného začlenenia, ktorú navrhol Eshelby (8), a jej rozšírenie, Moriho/Tanakova teória (9), sa dá použiť na viac kompozitných materiálov ako pravidlo miešania, ale jej účinnosť nie je dostatočne preukázaná s výnimkou kompozitných materiálov s nespojitými vláknami, ako sú napríklad vstrekované výrobky, pretože teoretický vývoj je založený na predpoklade, že tvar začlenenia je sféroid. Metóda homogenizácie (10) použitá v tomto článku priťahuje pozornosť ako metóda, ktorá môže vyriešiť tieto problémy. Pri homogenizačnej metóde sa model, ktorý reprezentuje mezoškálovú štruktúru kompozitného materiálu (v prípade GFRP veľkosť, pri ktorej možno pozorovať heterogénnu štruktúru vlákien a živice), používa na simuláciu skúšky materiálu pomocou metódy konečných prvkov a numerická skúška sa vykonáva na vyhodnotenie zdanlivej odozvy materiálu a na meranie vlastností materiálu. Keďže interakciu medzi vláknami možno dôkladne zohľadniť, uvedený problém možno riešiť všeobecne pre akýkoľvek kompozitný materiál.
V posledných rokoch je silná tendencia aktívne využívať nové materiály s cieľom zlepšiť vlastnosti výrobkov a na trh sa postupne uvádzajú nové kompozitné materiály. Vďaka univerzálnosti metódy homogenizácie je najvhodnejším prístupom pre trendy na trhu s týmto materiálom. Podrobnosti o metóde homogenizácie nájdete v existujúcej aplikačnej poznámke č. 58 (11). Tu je dôležité zdôrazniť, že metóda homogenizácie si na vykonanie simulácií vyžaduje aj vstupné informácie, ako je tvar mikroštruktúry a materiálové vlastnosti jednotlivých vlákien a živíc. Inými slovami, problém získania fyzikálnych vlastností sa nedá vyriešiť len technológiou analýzy, ale vlastnosti kompozitných materiálov sa dajú určiť len kombináciou merania a analýzy.
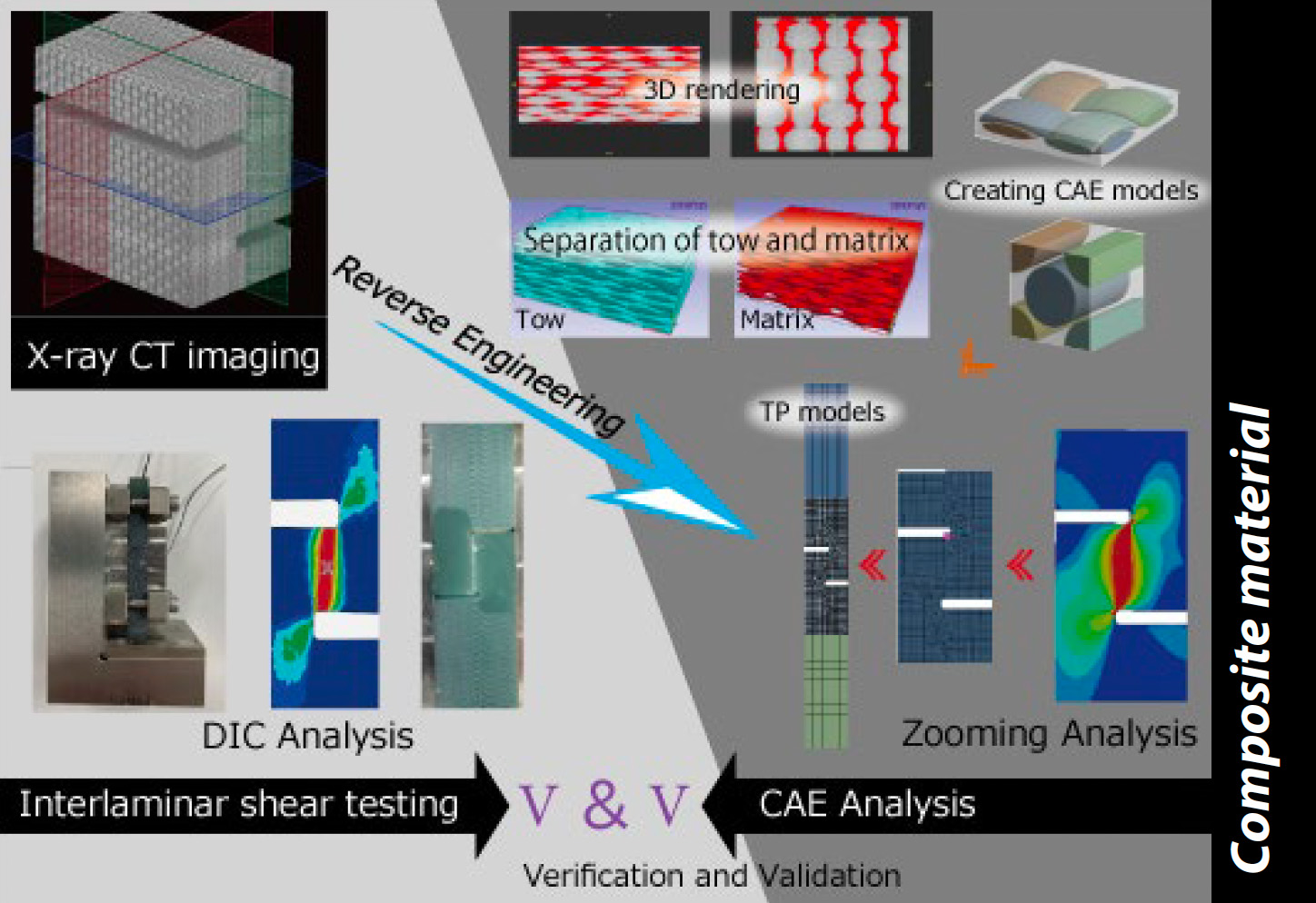
V aplikačnej poznámke č. 58 boli uvedené príklady overovania jednoosových ťahových vlastností kompozitných materiálov kombináciou merania a analýzy. V tomto článku sa pozornosť sústreďuje na režim šmykovej deformácie a uvádza sa príklad výskumu, ktorý kombinuje meranie a analýzu. Najprv bol vytvorený analytický model na základe výsledkov pozorovania heterogénnej mezoskalárnej štruktúry pomocou röntgenovej počítačovej tomografie (CT) a hodnoty vlastností boli predpovedané vykonaním homogenizačnej analýzy. Platnosť modelu sa overila porovnaním predpovedaných výsledkov so skutočnými výsledkami pre čistý strih. Okrem toho sa samostatne vykonala analýza, v ktorej sa pomocou koeficientu trenia reprodukovali obmedzujúce podmienky skúšobnej vzorky, ktoré boli spôsobené skúšobným prípravkom použitým v experimente (prípravok zodpovedajúci norme JIS K 7092). Analytické výsledky sa porovnali s experimentálnymi výsledkami s cieľom overiť platnosť experimentálnych výsledkov.
Určenie rôznych parametrov potrebných na vytvorenie modelu
Hodnotenie medzilamelových šmykových vlastností tkaných materiálov GFRP
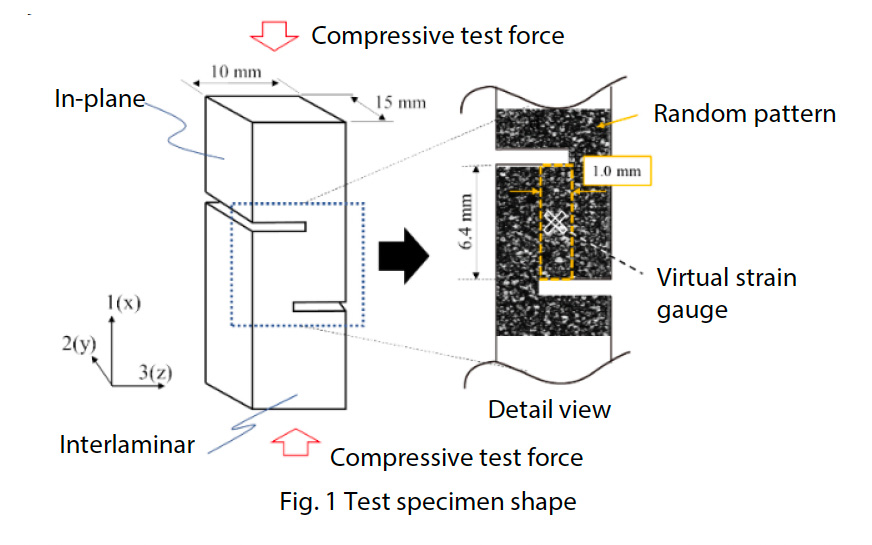
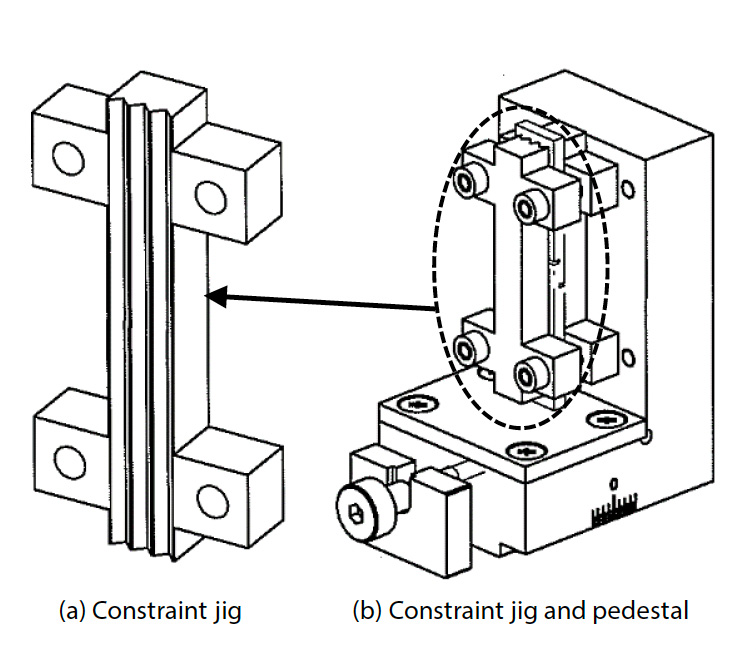
Ako je znázornené na obr. 1, skúšobná vzorka bola vyrobená z hladkej tkanej plochej dosky z GFRP s hrúbkou približne 10 mm. Celková dĺžka vzorky bola 80 mm a s cieľom koncentrovať šmykovú deformáciu medzi vrúbkovanými drážkami vystavenými šmykovému zaťaženiu sa vrúbkované drážky prekrývali o 1 mm, aby sa rozšírila oblasť šmykovej deformácie oproti tvaru špecifikovanému v JIS K 7092 (5), a rozloženie deformácie v oblasti šmykovej deformácie bolo rovnomerné (4). Šírka medzery medzi zárezovými drážkami bola navrhnutá na 1 mm. Na povrch skúšobnej vzorky bol nanesený náhodný vzor tak, že sa použil čierny sprej a následne biely sprej. Vzorka bola osadená do systému na skúšku medzilamelového šmyku, ktorý pozostával z prípravku vyhovujúceho norme JIS K 7092 a prítlačnej dosky s mechanizmom na nastavenie rovnobežnosti. 
γXZ=|ε_ (+45) |+|ε_ (-45) | (1)
|ε_ (+45) | : Absolútna hodnota deformácie získaná z výstupu virtuálneho tenzometra inštalovaného pod uhlom + 45°
|ε_ (-45) | : Absolútna hodnota deformácie získaná z výstupu virtuálneho tenzometra inštalovaného pod uhlom -45°
Nominálne šmykové napätie τXZ bolo vypočítané z rovnice (2).
τXZ= F/ab (2)
F: skúšobná sila (N), a: vzdialenosť medzi vrúbkovanými drážkami (6,4 mm), b: šírka vzorky (15 mm)
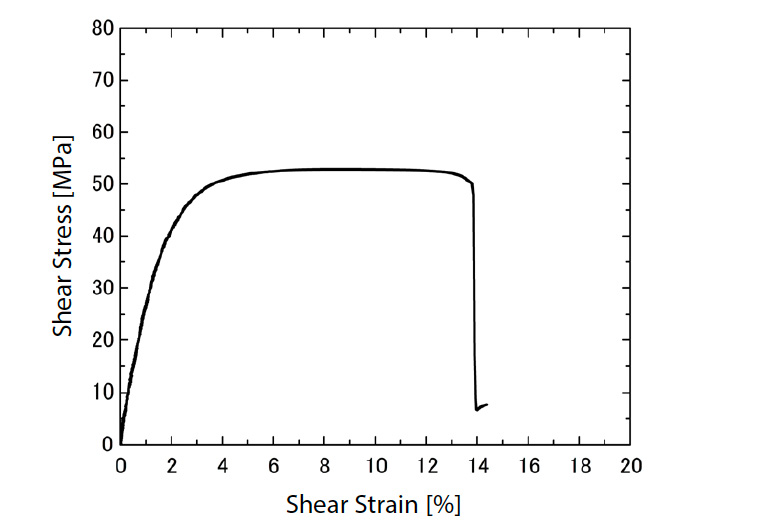
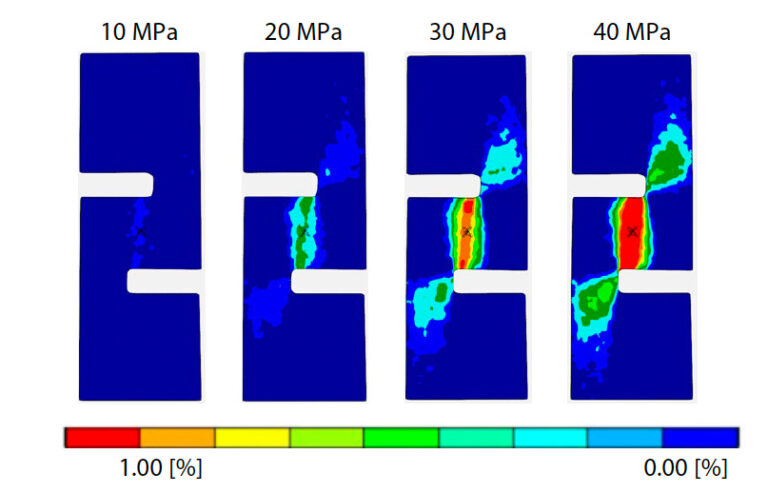
Na obr. 5 je znázornený diagram medzilamelového šmykového napätia a deformácie hladkého tkaného GFRP získaný pri tejto skúške. Vzťah medzi napätím a deformáciou jednoduchého tkaného GFRP je lineárny až do šmykového napätia približne 30 MPa, ale potom sa stáva nelineárnym a pri približne 50 MPa podľahne. Ako už bolo spomenuté, hladký tkaný materiál GFRP má štruktúru, v ktorej je laminovaná tkanina zo sklených vlákien impregnovaná živicou. Preto je GFRP hladký tkaný materiál bohatý na živicu v interlaminárnom smere a predpokladá sa, že nelinearita sa objavila v dôsledku charakteristík tvárnosti živice. Na obr. 6 sú znázornené obrysové diagramy medzilamelovej šmykovej deformácie z výsledkov DIC analýzy pri tlaku 10 až 40 MPa. Medzilamelová šmyková deformácia je od začiatku skúšky rovnomerne a široko rozložená medzi zárezy hladko tkaného materiálu GFRP a táto tendencia je rovnaká aj pri zvyšovaní zaťaženia pôsobiaceho na skúšobnú vzorku. Zo závislosti od napätia v lineárnej počiatočnej oblasti, od 0,1 do 0,3 % deformácie na obr. 5, bol modul medzilámového šmyku vypočítaný metódou najmenších štvorcov 2546,1 MPa.
Vyhodnotenie podmienok obmedzenia vzorky meraním koeficientu trenia
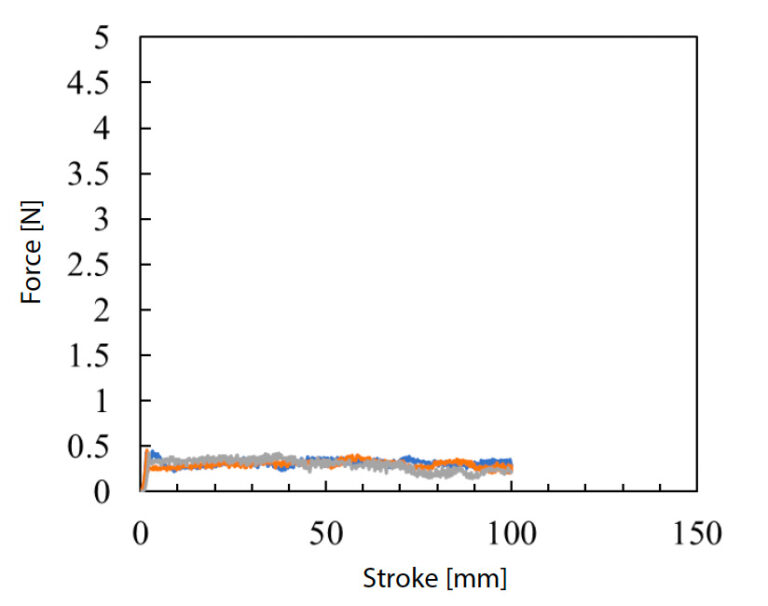
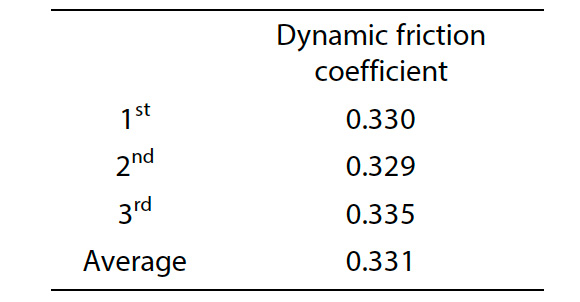
Obmedzujúce podmienky skúšobných vzoriek použitých pri skúške medzilamelového strihu sa odhadli meraním koeficientu trenia pomocou presného univerzálneho skúšobného stroja Autograph AGX-5NV a meracieho zariadenia koeficientu trenia. Na obr. 7 je znázornená skúška. Pri vykonávaní skúšky sa na skúšobný priestor skúšobného stroja po vyrezaní vzorky so zárezmi umiestnila plochá doska z hladko tkaného materiálu GFRP s hrúbkou 10 mm a na plochú dosku sa nainštaloval obmedzovací prípravok tak, aby sa jej dotýkala styčná plocha vzorky. Rýchlosť skúšky bola nastavená na 100 mm/min a údaje o skúšobnej sile sa získali pri zdvihu skúšobného stroja 100 mm. Na potvrdenie reprodukovateľnosti získaných údajov sa vykonali tri skúšky. Koeficient dynamického trenia na použitie v analýze CAE sa vypočítal z priemerných údajov o skúšobnej sile pre zdvih 20 až 60 mm získaných pri stabilnej skúšobnej sile a hmotnosti prípravku. Na obr. 8 je znázornený diagram závislosti skúšobnej sily od zdvihu a v tabuľke 1 sú uvedené výsledky výpočtu koeficientu dynamického trenia. Z uvedených výsledkov sa zistilo, že koeficient dynamického trenia vytvorený na kontaktnej ploche medzi vzorkou a obmedzovacím prípravkom je 0,33.
Získavanie údajov o tvare vzorky s vrúbkovaním pomocou röntgenového CT systému
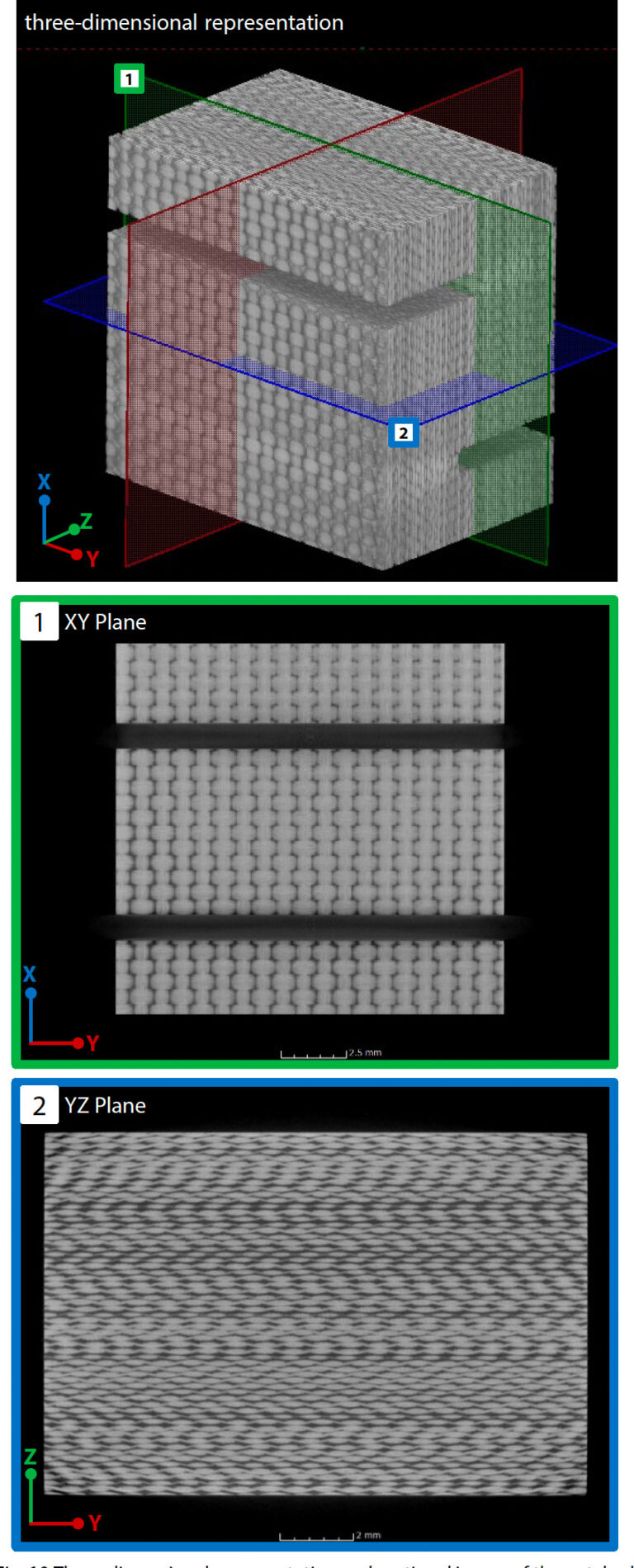
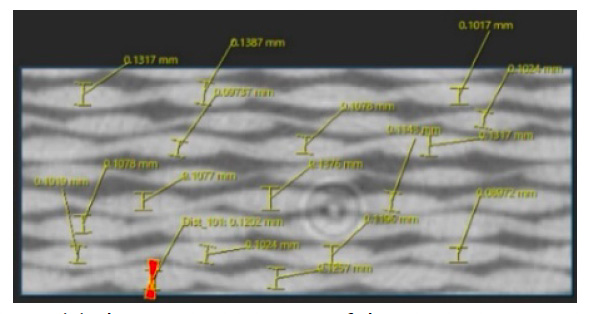
Pomocou mikroohniskového röntgenového CT systému inspXio™ SMX™-225 CT FPD HR Plus, ktorý je znázornený na obr. 9, sa získali snímky prierezu vzorky so zárezom na určenie tvaru analytického modelu. Za podmienok uvedených v tabuľke 2 sa zhotovili CT snímky v blízkosti zárezovej drážky skúšky a niekoľko stoviek prierezových snímok bolo vyvedených do formátu DICOM (Digital Imaging and Communications in Medicine). Na obr. 10 sú znázornené snímky prierezov a trojrozmerné zobrazenie vytvorené pomocou softvéru na trojrozmernú analýzu obrazu na základe snímok prierezov. Na priečnom reze sa oblasti s vysokou hustotou a vysokou absorpciou röntgenového žiarenia zobrazujú bielo a oblasti s nízkou hustotou a nízkou absorpciou röntgenového žiarenia sa zobrazujú čierno. Spracovanie obrazu sa vykonalo na vytvorenie modelu z prierezového obrazu na použitie v analýze konečných prvkov. Analýzou prierezových snímok získaných pomocou CT zobrazenia pomocou programu Simpleware™ vyrobeného spoločnosťou Synopsys sa identifikovali tvarové parametre mikroštruktúry potrebné na vytvorenie modelu analýzy. V prípade analyzovaného hladko tkaného materiálu GFRP sú faktormi, ktoré ovplyvňujú vlastnosti materiálu, objemový obsah a tvar priečneho rezu vlečky (zväzok niekoľkých stoviek až 1 000 vlákien usporiadaných v jednom smere) a vzdialenosť medzi susednými zväzkami vlákien. Obsah monofilamentov vo vnútri uteráka tiež ovplyvňuje vlastnosti materiálu, ale v tomto analytickom obraze nebolo možné získať jasný kontrast ani v jemnej oblasti vo vnútri uteráka, preto bol určený porovnaním s výsledkom montáže. Podrobnosti sú opísané v časti 3 nižšie. Tieto tvarové parametre nie sú v celom materiáli rovnomerné a sú rozložené s odchýlkami. Preto sa v nástroji na analýzu obrazu meral pomerne široký rozsah zahŕňajúci viacero zväzkov vlákien a priemerná hodnota sa prijala ako tvar modelu analýzy.
Vytvorenie modelu
Identifikácia tvarových parametrov
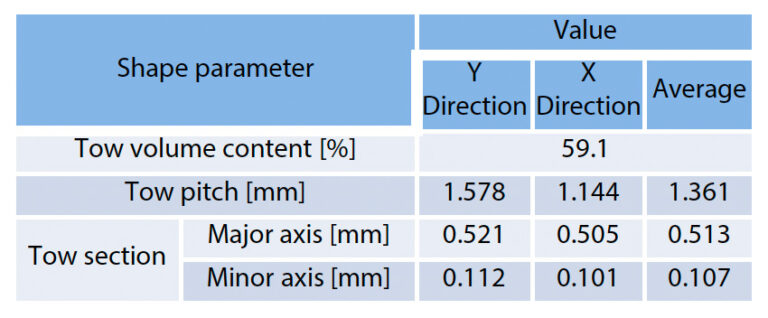
Na obr. 11 je znázornený objemový podiel vlečky nameraný programom Simpleware. Oblasť vlečky a oblasť matrice sa oddelili binarizáciou obrazu v stupňoch šedej získaného z röntgenového CT pomocou vhodných prahov. Objemový podiel sa určil meraním objemu každej oddelenej oblasti.
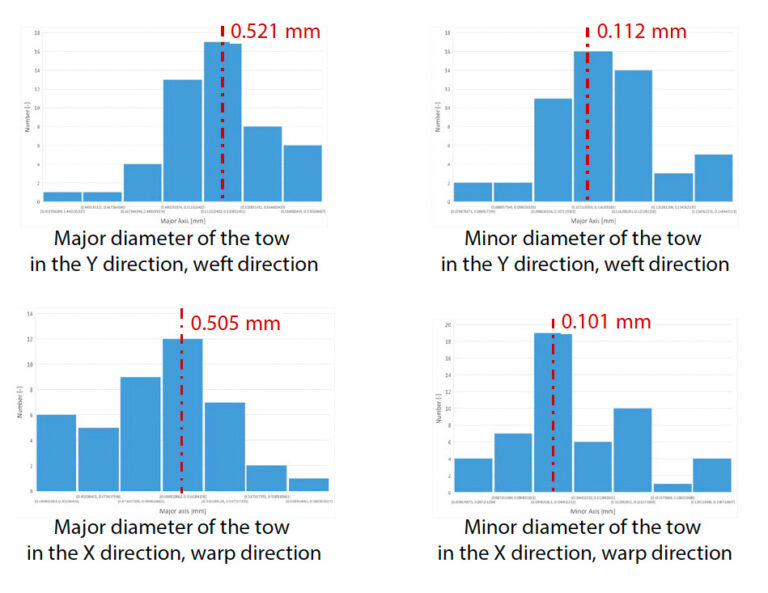
Na obr. 12 je znázornený tvar priečneho rezu vlečky a nameraná vzdialenosť medzi vlečkami. Predpokladalo sa, že vlek má eliptický prierez, a merali sa hlavné a vedľajšie priemery. Náhodne sa vybralo 49 vlečných sietí. Na obr. 12 je znázornený výsledok nakreslenia histogramu so 7 binármi uplatnením teorémy druhej odmocniny na počet meracích bodov pre každý nameraný parameter tvaru. Keďže nebola tendencia, aby sa všetky tvarové parametre jednoznačne zhodovali so všeobecnou štatistickou funkciou, ako je Gaussovo rozdelenie, ako tvarový parameter sa použila priemerná hodnota koša s najvyššou pravdepodobnosťou existencie. Z tohto výsledku vyplýva, že tvar ťahu v smere X a Y je zreteľne odlišný. Vo všeobecnosti je však veľmi zriedkavé navrhovať výrobok s ohľadom na tieto mikroštruktúry závislé od smeru, preto sa tentoraz použil ďalší priemer priemerných hodnôt v oboch smeroch rovnako pre ťah v oboch smeroch.
Na obr. 12 (c) je znázornený aj obraz merania vzdialenosti medzi susednými ťahmi. Tento tvarový parameter sa meral z mimoplošného obrazu. Hranica medzi oblasťami, ktoré nie sú zakryté kolmým vlekom, a oblasťami, ktoré sú zakryté kolmým vlekom, je bohatá na plastické látky, a preto sa javí tmavá. V dôsledku toho sa oblasti, ktoré nie sú zakryté kolmým vlečením, a oblasti, ktoré sú zakryté kolmým vlečením, javia ako samostatné obdĺžnikové tvary. Rozstup vlečných sietí bol definovaný ako vzdialenosť medzi stredovými bodmi tohto obdĺžnika. Rovnako ako pri tvare priečneho rezu vlečnej siete sa merala vzdialenosť medzi 49 vlečnými sieťami. V prípade rozstupu medzi ťahmi sa pozorovala tendencia závislosti od vertikálneho a zvislého smeru vlákien v bode c) na tom istom obrázku a potom sa do modelu analýzy použila priemerná hodnota. V tabuľke 3 a na obr. 13 sú zhrnuté jednotlivé nakoniec identifikované tvarové parametre a skutočne vytvorené analytické modely pre numerický test.
Optimalizácia tvarových parametrov
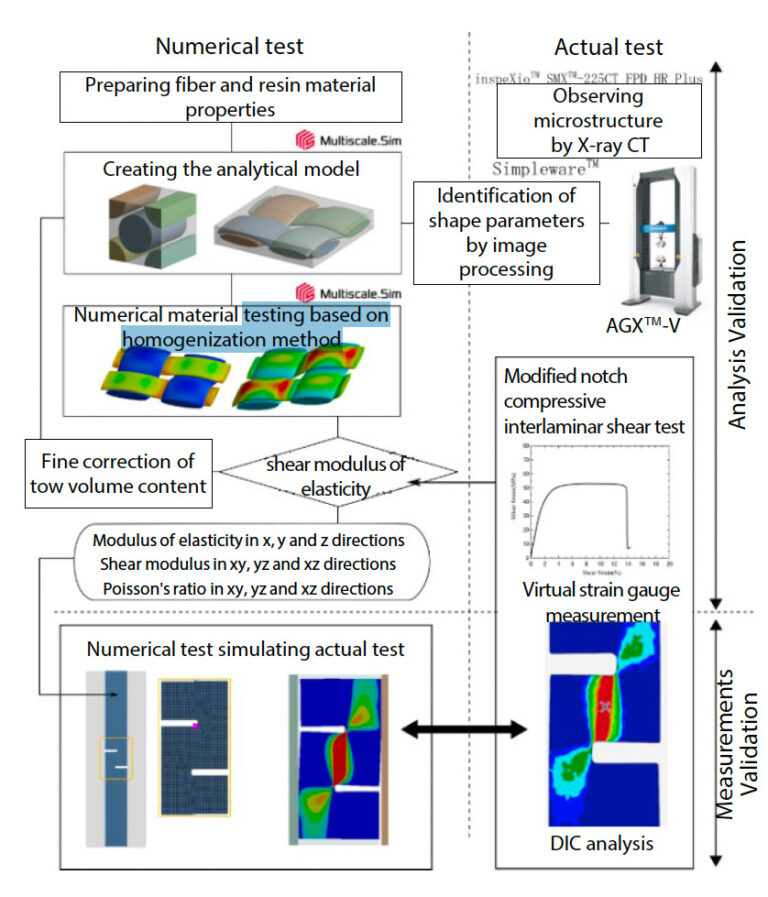
Materiály vystužené spojitými vláknami, ako je napríklad tkanina použitá v tejto analýze, majú tendenciu mať veľmi silnú anizotropiu. Analytické metódy založené na metóde homogenizácie (10) sú účinné na analytické predpovedanie vlastností materiálu, ktoré charakterizujú anizotropné správanie. Metóda homogenizácie poskytuje analytický prístup na vyhodnotenie zdanlivej odozvy materiálu a v konečnom dôsledku identifikáciu vlastností materiálu vykonaním numerickej skúšky. test numerickým výpočtom pomocou modelu konečných prvkov, ktorý reprezentuje nehomogenitu mikroštruktúry. Jednoduchým meraním materiálových vlastností jednotlivých vlákien a živíc (a vlastností materiálového rozhrania, ak sa majú zohľadniť) alebo ich získaním z databázy atď. možno získať anizotropné správanie materiálu a materiálové vlastnosti pre všetky typy výstuže na základe ich heterogénnej mikroštruktúry. Podrobnosti o tejto metóde analýzy sú uvedené v aplikačnej poznámke č. 58 (11). Celkový priebeh analýzy je znázornený na obr. 14. Uskutočnil sa pokus o overenie platnosti aspektov analýzy aj merania. Analytické overenie sa vykonalo pomocou vyššie opísanej homogenizačnej analýzy. Požadovanými informáciami bol tvar mikroštruktúry a vlastnosti materiálov, z ktorých bola zložená. Konkrétne hodnoty tvarových parametrov potrebných na modelovanie mikroštruktúry sa určili použitím údajov pozorovaných pomocou röntgenového CT na spracovanie obrazu, ako je opísané v časti 2 - 3.
Validácia testovacej metódy
Na overenie platnosti skutočnej skúšobnej metódy sa vykonala analýza s rovnakým tvarom a okrajovými podmienkami ako pri skúške. Materiálové vlastnosti hladkého látkového materiálu použitého v tomto modeli analýzy boli získané vo fáze overovania analýzy. Porovnaním rozloženia šmykovej deformácie vo vzorke získanej analýzou s výsledkom nameraným analýzou DIC sa potvrdilo, že analytický výsledok sa dobre zhoduje so skutočným výsledkom skúšky. Zároveň sa na strane analýzy pokúsili kvantifikovať podmienky ovplyvňujúce výsledky skúšky porovnaním koeficientu trenia medzi prípravkom a vzorkou a analytických výsledkov získaných praktickou zmenou uťahovacieho zaťaženia prípravku.
Metóda analýzy
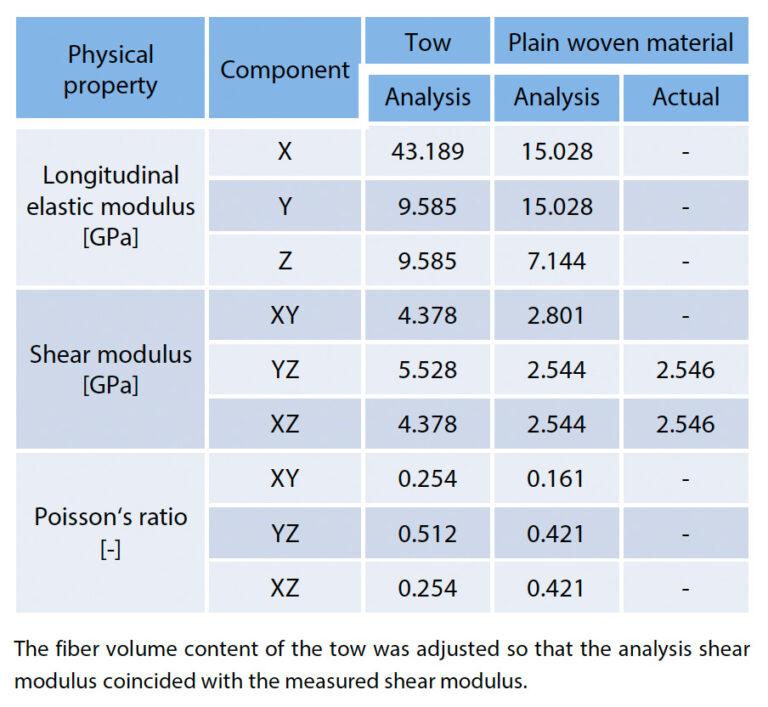
Najprv sa vypočítali ortotropné materiálové vlastnosti GFRP tkaných materiálov pomocou homogenizačnej analýzy. Na obr. 15 sú znázornené modely pevných telies a konečných prvkov materiálu GFRP tkaniny, ktoré sa použili pri analýze. Ako už bolo uvedené, mezoškály tkaných štruktúr boli identifikované spracovaním obrazu z výsledkov získaných pomocou röntgenového CT. Model mezoškály predpokladá, že oblasť ťahadla je homogénna. V skutočnosti má materiál nehomogénnu štruktúru pozostávajúcu zo zväzkov vlákien orientovaných v jednom smere, preto je potrebné zabezpečiť anizotropné vlastnosti materiálu, ktoré správne odrážajú mikroskopickú štruktúru. Preto sa model znázornený na obrázku (a-2) a obr. (b-2) bol pripravený pre zväzky vlákien v oblasti ťahu a na získanie fyzikálnych vlastností sa samostatne vykonala homogenizačná analýza. Materiály, ktoré tvoria kompozit, sú sklo E (Youngov modul: 72,5 GPa, Poissonov pomer: 0,2) pre vlákna a epoxidová živica (Youngov modul: 3,5 GPa, Poissonov pomer: 0,35) pre živice. Predpokladalo sa, že obidve tieto vlastnosti sú pružné, a odkázalo sa na hodnoty v databáze materiálov, ktorú poskytol nástroj na analýzu. Pri homogenizačnej analýze sa všetky materiálové vlastnosti charakterizujúce ortotropné vlastnosti materiálov z GFRP tkanín získali vykonaním numerických skúšok simulujúcich ideálny jednoosový ťah a medzilamelový strih pre tieto modely. Konkrétne materiálové vlastnosti pozostávali z 9 druhov fyzikálnych vlastností: pozdĺžny modul pružnosti, Poissonov pomer a modul pružnosti v šmyku v 3 smeroch. Na obr. 16 je znázornený analytický model vykonaný na overenie experimentálnej strany. Model pozostával zo vzorky GFRP a obmedzovacieho prípravku, ktorý drží vzorku v smere hrúbky. Tlakové zaťaženia a tlakové napätia na vzorkách a prípravkoch boli definované priamo na plochách týchto častí a ostatné geometrické prvky (otvory pre skrutky prípravku, prípravok na podopretie vzorky z hornej a dolnej časti obrázka atď. dôsledne modelované. Konkrétne, spodný povrch vzorky na obr. 16 bol definovaný s plným posunutím a horný povrch bol definovaný s tlakovým napätím 30 MPa. Pri skutočnej skúške sa prostredníctvom krútiaceho momentu pôsobiaceho na prípravok aplikovalo tlačné zaťaženie v smere mimo roviny, ale v analýze bol posun prípravku obmedzený na nulu. Okrem toho sa analyzoval aj prípad, keď prípravok nebol nainštalovaný. V blízkosti zárezu GFRP sa očakávalo zložité rozloženie deformácií, ale v oblasti dostatočne vzdialenej od zárezu sa očakávalo takmer rovnomerné rozloženie napätí a deformácií. Preto bola časť z GFRP rozdelená na oblasť v blízkosti zárezu a ostatné oblasti a sieť bola jemne nastavená len v blízkosti zárezu. Medzi dvoma časťami s rôznou hrubosťou siete existovala nespojitá sieť, ale realistický stav pripojenia sa reprodukoval definovaním viacbodového obmedzenia (MPC) na rozhraní. Pokiaľ ide o správanie materiálu, dielu z GFRP boli pridelené materiálové vlastnosti získané homogenizačnou analýzou uvedenou vyššie a predpokladalo sa, že prípravok je tuhý a nedeformovateľný. Koeficient trenia medzi rovinným tkaným materiálom GFRP a prípravkom sa analyzoval v 3 vzorkách, 0,0, 0,3 a 0,4, aby sa potvrdil vplyvna výsledky skúšky. Z údajov o výsledkoch analýzy, ktoré sa tu získali, sa pozorovalo rozloženie medzilamelovej šmykovej deformácie a hodnoty šmykovej deformácie a šmykového napätia v strede vzorky. Platnosť skúšobných podmienok sa overila porovnaním týchto výsledkov s nameraným rozložením šmykovej deformácie získaným pomocou analýzy DIC a nameranou šmykovou deformáciou v strede vzorky získanou pomocou virtuálneho tenzometra. Pri tejto skúške sa v ideálnom prípade tlakové napätie 30 MPa pôsobiace na hornú časť vzorky prenáša ako šmykové napätie v strede vzorky. Vo výsledkoch analýzy sa sledovalo šmykové napätie, aby sa zistilo, či sa tento ideálny stav dosiahol.Výsledky analýzy CAE
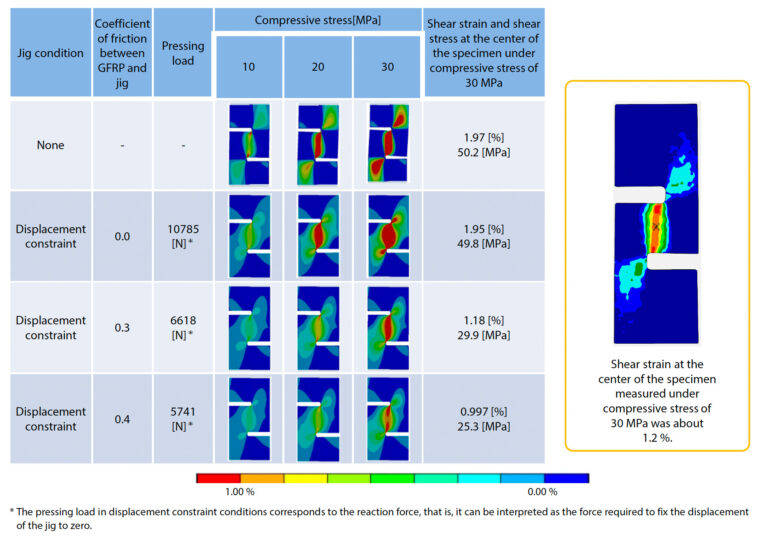
Najprv sa vykonala homogenizačná analýza na analytickom modeli znázornenom na obr. 16 a výsledky vyhodnotenia ortotropných modulov pružnosti oblasti vlečky a celého hladko tkaného materiálu sú uvedené v tabuľke 4. Keďže pri skúške sa vyhodnocovala šmyková tuhosť rovinného tkaného materiálu, v analýze sa upravil objemový obsah vlákien v oblasti kúdele tak, aby sa modul šmyku analýzy zhodoval s nameraným modulom šmyku. Objemový obsah vlákien v oblasti vlečky, ktorý sa nakoniec získal inverzným odhadom, bol približne 57,27 %. Tento údaj sa veľmi nelíšil od iných štúdií vykonaných pomocou SEM a považuje sa za primeraný. V tabuľke 5 sú zhrnuté výsledky jednotlivých prípadových štúdií, v ktorých sa optimalizovaný model použil na zmenu prítomnosti alebo neprítomnosti obmedzovacieho prípravku a na zmenu koeficientu trenia medzi obmedzovacím prípravkom a vzorkou. Výsledky nameraného rozloženia šmykovej deformácie z analýzy DIC sú uvedené aj v pravej a vonkajšej časti tabuľky 5. Za všetkých podmienok je vidieť, že šmyková deformácia je sústredená v blízkosti stredu vzorky umiestnenej medzi dvoma zárezmi. Možno však usudzovať, že deformácia vzorky je odlišná, pretože rozloženie deformácie závisí od podmienok namáhania v oblasti mierne vzdialenej od stredu a na okrajovej strane dvoch zárezov. Keď nie je nainštalovaný prípravok, je vidieť, že existuje vysoká deformácia rovnakého rádu ako v strede vzorky, ktorá sa rozširuje od zárezu k okraju. Môže to byť spôsobené deformáciou vzorky mimo roviny. Z výsledkov tiež vyplýva, že šmykové napätie v strede vzorky je väčšie ako vonkajší tlak, čo naznačuje, že presnú mimorovinnú šmykovú deformáciu nemožno dosiahnuť. Za podmienok, keď je umiestnená pevná prípravok, je oblasť vysokého šmykového napätia na koncovej strane od zárezu malá, takže je vidieť, že deformácia pri vybočení je potlačená. Potvrdilo sa, že stupeň potlačenia je výraznejší, keď sa zvyšuje koeficient trenia medzi hladkým tkaným materiálom GFRP a prípravkom. Keď sa však koeficient trenia zvýšil na 0,4, napätie v strede vzorky sa stalo menším ako vonkajší tlak. Predpokladá sa, že je to spôsobené tým, že energia vonkajšieho tlaku sa stráca v dôsledku odporovej sily trenia v miere, ktorú nemožno ignorovať. Pri skutočnej skúške sa koeficient trenia nedá kontrolovať, preto je potrebné použiť vhodné tlakové zaťaženie, aby sa deformácia v rovinnom smere príliš nepotlačila a zároveň sa potlačilo vybočenie vzorky mimo roviny.
Pri skúške opísanej v časti 2-2 sa potvrdilo, že koeficient trenia medzi materiálmi je približne 0,3. Za týchto podmienok sa šmykové napätie v strede vzorky rovná vonkajšiemu tlaku, čo znamená, že sa dosiahli ideálne šmykové podmienky.
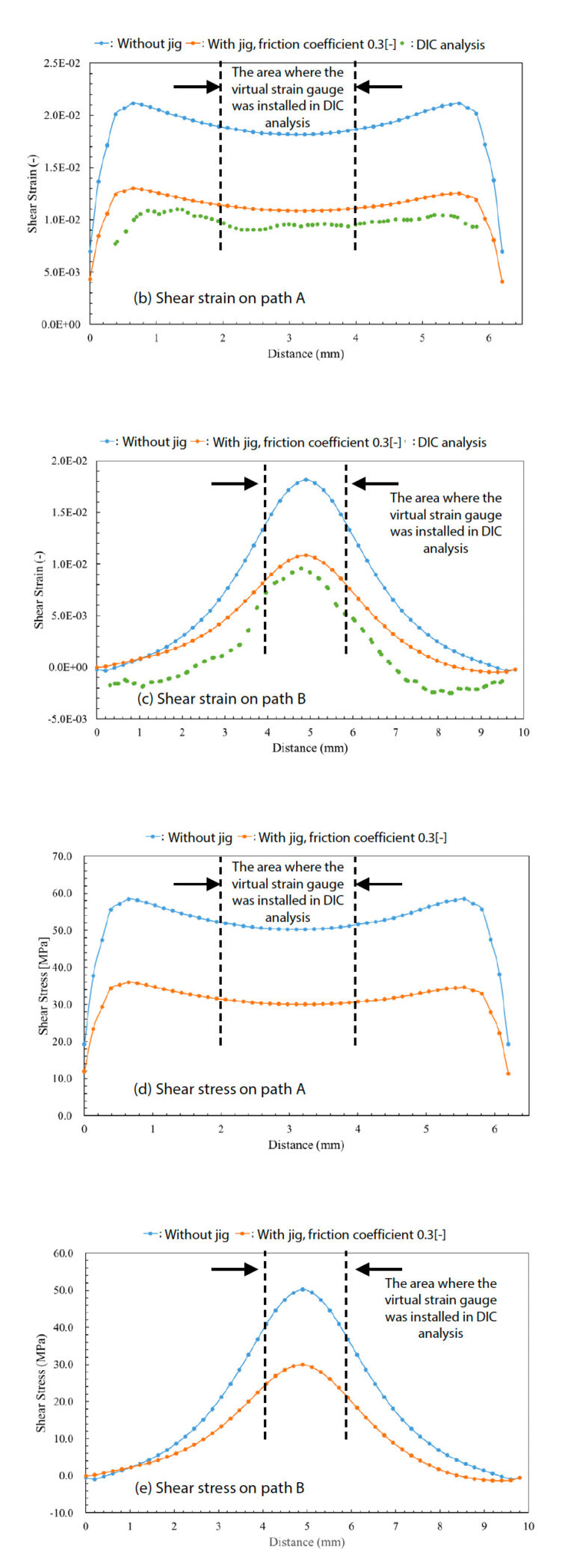
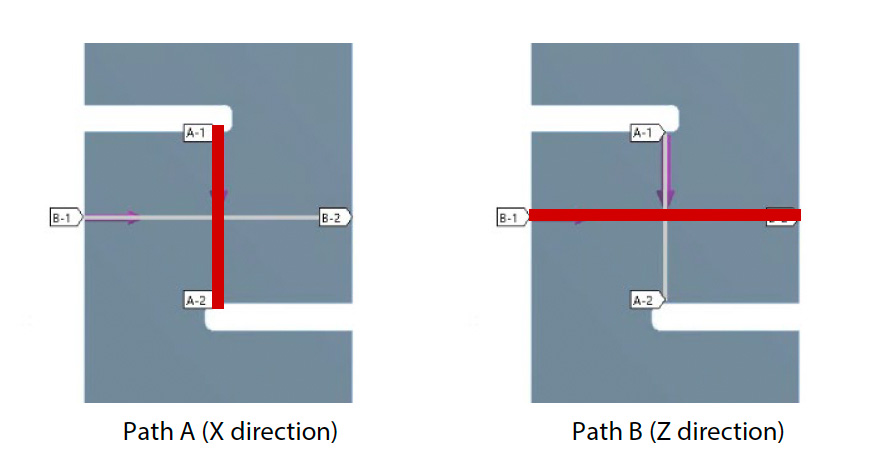
Nakoniec, aby sme videli rozloženie šmykovej deformácie v blízkosti zárezov podrobnejšie, boli výsledky šmykovej deformácie a šmykového napätia vynesené na 2 dráhy znázornené na obr. 17 (a). Výsledky sú znázornené na obr. b) až e). Stred vzorky zodpovedá vzdialenosti 3,2 mm v dráhe A a 5,0 mm v dráhe B. V analýze DIC sa oblasť, kde bol nainštalovaný virtuálny tenzometer, nachádza v blízkosti stredu. Pre presnú skúšku medzilamelového šmyku sa očakáva, že centrálna časť vzorky je v ideálnom režime šmyku, ale je tiež žiaduce, aby podobné podmienky existovali v širokom rozsahu v okolí. Najmä pri meraní lokálnych hodnôt deformácie tenzometrom je žiaduce udržiavať konštantnú hodnotu v oblasti merania približne 2 mm x 2 mm.
V stave, keď je umiestnený obmedzovací prípravok, ako je znázornené na obr. 17 (b) a (c), sa to takmer dosiahne a očakáva sa, že medzilamelové šmykové charakteristiky vzorky možno merať s určitou presnosťou. Na druhej strane, v prípade, že prípravok nie je umiestnený, v dôsledku vybočenia mimo roviny je stredná šmyková deformácia abnormálne veľká v porovnaní s meraním a výsledok na dráhe A je pozoruhodne vypuklý smerom nadol, ako je znázornené na obr. 17 (b).
Kontrolovalo sa aj rozloženie šmykového napätia a zistilo sa, že za podmienok, keď bol umiestnený obmedzovací prípravok, bolo šmykové napätie znázornené na obr. 17 (d) do určitej miery široko rozložené na dráhe A podobne ako šmyková deformácia. Okrem toho sa potvrdilo, že virtuálny tenzometrický snímač použitý v analýze DIC bol široko rozložený v oblasti, kde bol virtuálny tenzometrický snímač nainštalovaný na dráhe B, ktorá sa nachádzala blízko stredu medzi vrúbkovanými drážkami zodpovedajúcimi vzdialenosti 2 až 4 mm na dráhe B. Pri skúške neexistuje iná metóda na vyhodnotenie napätia ako výpočet nominálneho šmykového napätia vydelením skúšobnej sily nameranej v snímači zaťaženia skúšobného stroja plochou prierezu vzorky, ako je uvedené v rovnici (2) v časti 2-1. Vo výsledkoch zobrazených na obr. 17(d) nie je v blízkosti zárezu vo vzorke žiadna koncentrácia napätia a rovnomerné rozloženie napätia v intervale zárezu 6,4 mm možno overiť len pomocou analýzy CAE. Výsledky analýzy CAE nepreukázali žiadnu významnú lokálnu koncentráciu napätia, čo poskytuje dôkaz, že skúšobné metódy a skúšobné geometrie použité v skúške sú užitočné na vyhodnotenie nominálneho šmykového napätia, ako aj lineárnej a nelineárnej deformácie.
Tieto výsledky naznačujú, že skúšku medzilamelovým šmykom možno reprodukovať umiestnením prípravku v smere mimo roviny vzorky a jeho podopretím miernym zaťažením, ktoré nenarušuje tangenciálny sklz materiálového rozhrania nástroj - vzorka, ale potláča normálne vybočenie.
Zhrnutie
V tomto príspevku sme predstavili prípad, v ktorom sa vyhodnotili medzilámové šmykové charakteristiky hladko tkaných materiálov GFRP metódou medzilámovej šmykovej skúšky s použitím modifikovanej metódy vrubovej kompresie z experimentálnej analýzy DIC aj analýzy CAE.
Model analýzy CAE bol vytvorený nastavením okrajových podmienok medzi vzorkou a obmedzovacím prípravkom s prihliadnutím na koeficient trenia. Zistilo sa, že výsledky analýzy DIC a analýzy CAE sú takmer identické v nasledujúcich troch bodoch získaných medzi vrubovými drážkami vzorky.
1. Obrysový diagram rozloženia šmykovej deformácie
2. Tvar rozloženia šmykovej deformácie v smere X
3. Tvar rozloženia šmykovej deformácie v smere Z
Okrem toho bolo rozloženie napätia medzi zárezovými drážkami vypočítané analýzou CAE široké a rovnomerné a nebola pozorovaná žiadna lokálna koncentrácia napätia.
Metóda skúšky medzilamelovým šmykom s modifikovaným vrubovým stlačením použitá pri skutočnej skúške sa ukázala ako užitočná nielen na získanie lineárnej a nelineárnej deformácie, ale aj na vyhodnotenie nominálneho šmykového napätia.
Odkazy
1) Pettersson KB, Neumeister JM. Ťahová súprava pre skúšku kompozitného strihu IDNS. Compos Part A Appl Sci Manuf 2006; 37 (2) : 229-42.2) Melin LN, Neumeister JM. Meranie konštitutívneho správania ortotropných kompozitov v šmyku a hodnotenie modifikovaného Iosipescuovho testu. Compos Struct 2006; 76 (1-2): 106-15.
3) Julio F. Davalos a, Pizhong Qiao b, Vinod Ramayanam a, Luyang Shan b, Justin Robinso. Torzia voštinových FRP sendvičových nosníkov so sínusoidnou konfiguráciou jadra. Compos Struct 2009; 88: 97-111
4) T.Murakami, T.Matsuo, T.Sumiyama, Experimental method and evaluation for interlaminar shear properties of randomly oriented strand thermoplastic composites based on modified double-notch specimen and two dimensional digital image correlation. J. Compos. Mater., v tlači, https://doi.org/10.1177/0021998320967719 (2020).
5) JIS K 7092. Skúšobná metóda na stanovenie pevnosti v medzilamelovom šmyku plastov vystužených uhlíkovými vláknami pomocou dvojzárezovej vzorky. In: Zborník z medzinárodnej konferencie o bezpečnosti a ochrane zdravia pri práci: JIS handbook. Tokio: Japonská asociácia pre normalizáciu; 2010.
6) Bouette B, Cazeneuve C a Oytana C. Effect of strain rate on interlaminar shear properties of carbon/epoxy composites. Compos Sci Technol 1992; 45: 313-321.
7) Internetová stránka Ministerstva hospodárstva, obchodu a priemyslu: https://www.meti.go.jp/policy/digital_transformation/index.html
8) J.D.Eshelby, The determination of the elastic field of an elipsoidal inclusion and related problems (Určenie elastického poľa elipsoidickej inklúzie a súvisiace problémy), Proc. Roy. Soc. Lond, zväzok A241, s. 376 - 396 (1957).
9) T. Mori, K. Tanaka, verage stress in matrix and average elastic energy of materials with misfitting inclusions, Acta Metallurgica, Vol.21, No.5, pp.571- 574 (1973).
10) Terada, K., Kato, J., Hirayama, N., Inugai, T. a Yamamoto, K., A method of two-scale analysis with micromacro decoupling scheme: application to hyperelastic composite materials, Computational Mechanics, Vol.52, pp.1199-1219 (2013).
11) Koji Yamamoto, Takashi Murakami, Satoshi Iguchi, Zen Miyazaki Application Note No.58 Overovanie a validácia (V&V) výsledkov simulácie jednoosovej ťahovej skúšky kompozitných materiálov: Fúzia skutočného merania a homogenizačnej analýzy https://www.shimadzu.com/an/sites/shimadzu.com.an/files/pim/pim_d ocument_file/applications/application_note/11055/jpi320003.pdf
12) https://www.cybernet.co.jp/ansys/product/lineup/multiscale/multiscale/
13) https://www.cybernet.co.jp/ansys/product/
Stiahnite si
- Aaplikácia: Validácia použiteľnosti modifikovanej metódy skúšky medzilomínového tlaku v záreze v šmyku
English 
German 
Czech 
Slovak 
Bulgarian 
Romanian 