Abstrakt
Wir untersuchten die Anwendbarkeit der modifizierten interlaminaren Kerbdruck-Scherprüfmethode, die für die Ermittlung der interlaminaren Schereigenschaften von thermoplastischem CFK geeignet ist, auf GFK-Gewebe, die in der Industrie weit verbreitet sind. Ein CAE-Analysemodell wurde auf der Grundlage der Ergebnisse der mesoskaligen Strukturbeobachtung durch Röntgen-CT erstellt, und es wurde eine Homogenisierungsanalyse durchgeführt, die sich auf die Zwangsbedingungen des Probekörpers unter dem Gesichtspunkt des Reibungskoeffizienten konzentrierte. Die gemessenen Werte und die Analyseergebnisse zeigten eine gute Übereinstimmung.
Einführung
In den letzten Jahren wurden glasfaserverstärkte Kunststoffe (GFK), die eine hohe spezifische Festigkeit und eine hervorragende Verarbeitungs- und Formbarkeit aufweisen, in großem Umfang für elektronische Substrate, Schiffe und Kfz-Außenteile verwendet und sind zu einem unverzichtbaren Material geworden. GFK ist ein Verbundwerkstoff mit Anisotropie und zeigt ein kompliziertes Verformungs- und Bruchverhalten, das von der Richtung der Hauptbelastungsachse abhängt: Zug, Druck, Biegung, Scherung in der Ebene, interlaminare Scherung und Scherung außerhalb der Ebene oder eine Kombination dieser Eigenschaften. Bei der Konstruktion von Produkten mit Hilfe von Computer Aided Engineering (CAE) besteht ein großer Bedarf an Prüfverfahren, mit denen das Versagensverhalten jedes einzelnen Bauteils bewertet werden kann.
*1 Cybernet Systems Co, Ltd. Abteilung Mechanik CAE.
*2 SHIMADZU CORPORATION
Der flammhemmende Typ 4 (FR4), der aus Glasfasern und Epoxidharz besteht, wird häufig in Leiterplatten für elektronische Geräte verwendet.
Der Hintergrund für den häufigen Einsatz von FR4 ist die Tatsache, dass das GFK-Gewebe hohe elektrische Isolationseigenschaften und Nichtentflammbarkeit aufweist und sich die Oberfläche aufgrund der verstärkenden Wirkung der Glasfasern bei Wärmeeinwirkung kaum verändert. Da dieses Material jedoch eine laminierte Struktur hat, sind die Fasern in der Ebene orientiert, aber es gibt fast keine Faserorientierung zwischen den Laminaten, was es zu einer harzreichen Struktur macht. Während die mechanischen Eigenschaften in der Ebene ausgezeichnet sind, ist die Verstärkungswirkung der Fasern in der interlaminaren Richtung schwach, so dass die physikalischen Eigenschaften des Matrixharzes vorherrschen und ein nichtlineares Verhalten aufgrund der Fließfähigkeit des Harzes zu erwarten ist. Es ist wichtig, die interlaminaren Schereigenschaften genau zu verstehen, um das Verformungsverhalten, das stark von den Eigenschaften des Matrixharzes abhängt, wie z. B. Biegen und Schälen, durch numerische Simulationen zu reproduzieren.
Mehrere Prüfverfahren wurden als repräsentative Methoden zur Messung der interlaminaren Schereigenschaften von Verbundwerkstoffen vorgeschlagen (1-3). Bei jeder Prüfmethode ist die Form der Vorrichtung kompliziert, und es ist schwierig, einen Probekörper für eine interlaminare Scherprüfung herzustellen, da die Größe des Probekörpers in Bezug auf die Laminierungsrichtung des Verbundwerkstoffs lang sein muss
(4). Die interlaminare Scherfestigkeitsprüfung durch Kerbdruck, bei der eine Druckbelastung auf die Endfläche eines kleinen Probekörpers ausgeübt wird, wie sie in JIS K 7092 beschrieben wird, ist eine weit verbreitete Prüfmethode, mit der die interlaminare Scherfestigkeit von kohlenstofffaserverstärkten Kunststoffen (CFK) leicht bewertet werden kann.
(5). Die für diese Prüfung erforderliche Probekörpergröße in Laminierrichtung beträgt nur 3,5 bis 6,5 mm, so dass die Herstellung von Probekörpern mit geringem Materialeinsatz problemlos möglich ist. Allerdings kann mit dieser Prüfmethode die Scherdehnung nicht ermittelt werden, da der Bereich, in dem sich die interlaminare Scherdehnung konzentriert, sehr schmal ist.
Was jedoch die Druckprüfung von duroplastischem CFK betrifft, so wurde in der bisherigen Forschung
(6) Es wurde durch Berechnungen vorgeschlagen, dass der interlaminare Scherdehnungsbereich durch eine größere Überlappung der Kerbnuten erweitert werden kann. In den letzten Jahren wurden Beispiele für modifizierte gekerbte interlaminare Druckscherversuche veröffentlicht, bei denen der interlaminare Scherdehnungsbereich durch Vertiefung der gekerbten Nut eines Probekörpers erweitert werden kann und ein Dehnungsmessstreifen im Verformungsbereich angebracht werden kann
(4). Es wurde festgestellt, dass die nichtlinearen Eigenschaften der interlaminaren Scherung direkt aus der berechneten nominalen Scherspannung, die durch Division der von der Prüfmaschine erhaltenen Druckkraft durch die Scherfläche zwischen den gekerbten Rillen erhalten wurde, und der gemessenen Dehnung, die mit dem Dehnungsmessstreifen erhalten wurde, ermittelt werden können. Bei dieser Prüfmethode wurde eine mit der Prüfmaschine synchronisierte Digitalkamera verwendet, um kleine Bereiche zu beobachten und zu bewerten, und die Dehnungsmessung wurde mittels digitaler Bildkorrelationsanalyse (DIC) durchgeführt. Durch die Verwendung der DIC-Analyse für die Dehnungsmessung wurde festgestellt, dass die interlaminare Scherdehnung von einer kleinen bis zu einer großen Verformung leicht gemessen werden kann, ohne dass man sich Gedanken über das Abfallen oder die Messgrenzen während der DMS-Messung machen muss. In diesem Beitrag wird untersucht, ob die modifizierte Kerbdruckprüfmethode, mit der sich die interlaminaren Schereigenschaften von thermoplastischem CFK effektiv ermitteln lassen, auch auf einfach gewebtes GFK, ein in der Industrie weit verbreitetes endlosfaserverstärktes Material, anwendbar ist.
Andererseits haben die Bemühungen, einen Teil der tatsächlichen Tests durch numerische Simulationen (CAE-Analysen) zu ersetzen, als Reaktion auf die Senkung verschiedener Kosten im Zusammenhang mit der Herstellung von Prototypen und die jüngste Bewegung zur Förderung der digitalen Transformation (7) im Zusammenhang mit dem neuen Coronavirus-Problem an Bedeutung gewonnen. Die für eine CAE-Analyse erforderlichen Eingabedaten lassen sich grob in drei Arten unterteilen: Analysemodelle, Materialeigenschaften und Randbedingungen. Insbesondere ist es sehr schwierig, Materialeigenschaften für Verbundwerkstoffe mit Anisotropie zu erhalten. Das elastische Verhalten isotroper Materialien wird durch vier Eigenschaften charakterisiert: Elastizitätsmodul, Poisson-Zahl, Schermodul und Volumenmodul. Im Allgemeinen werden der Elastizitätsmodul und die Poissonzahl, die experimentell leicht zu messen sind, als Eingangswerte verwendet, und die Messung des Schermoduls ist nicht erforderlich. Bei anisotropen Materialien sind Elastizitätsmodul und Schermodul jedoch unabhängig voneinander und müssen unabhängig voneinander gemessen werden.
Parallel zu den Bemühungen, den Schermodul, wie oben beschrieben, durch Versuche zu ermitteln, wurden viele Studien zur analytischen Vorhersage von Materialeigenschaften durchgeführt.
Die Mischungsregel (8), die als die klassischste Methode bekannt ist, ermöglicht die Vorhersage von Materialeigenschaften durch einfache Berechnungen, die manuell durchgeführt werden können. Die Mischungsregel geht jedoch davon aus, dass die Fasern und Harze, aus denen der Verbundwerkstoff besteht, in Reihe oder parallel zur Richtung der Belastungsachse geschaltet sind, oder anders gesagt, es werden zur Vereinfachung der Berechnung idealisierte Bedingungen angenommen, so dass sie nur auf sehr begrenzte Verbundwerkstoffe wie unidirektionale Verstärkung angewendet werden kann. Die von Eshelby (8) vorgeschlagene Methode des äquivalenten Einschlusses und ihre Erweiterung, die Mori/Tanaka-Theorie (9), können auf mehr Verbundwerkstoffe angewandt werden als die Mischungsregel, aber ihre Wirksamkeit ist außer bei Verbundwerkstoffen mit diskontinuierlichen Fasern, wie z. B. Spritzgussprodukten, nicht ausreichend nachgewiesen, da die theoretische Entwicklung auf der Annahme beruht, dass die Einschlussform ein Sphäroid ist. Die in dieser Arbeit angewandte Homogenisierungsmethode (10) erregt Aufmerksamkeit als eine Methode, die diese Probleme lösen kann. Bei der Homogenisierungsmethode wird ein Modell, das die mesoskalige Struktur eines Verbundwerkstoffs darstellt (im Falle von GFK die Größe, bei der die heterogene Struktur von Fasern und Harz beobachtet werden kann), zur Simulation einer Materialprüfung mit der Finite-Elemente-Methode verwendet, und es wird eine numerische Prüfung durchgeführt, um das scheinbare Materialverhalten zu bewerten und die Materialeigenschaften zu messen. Da die Wechselwirkung zwischen den Fasern genau berücksichtigt werden kann, lässt sich das obige Problem für jeden Verbundwerkstoff generisch lösen.
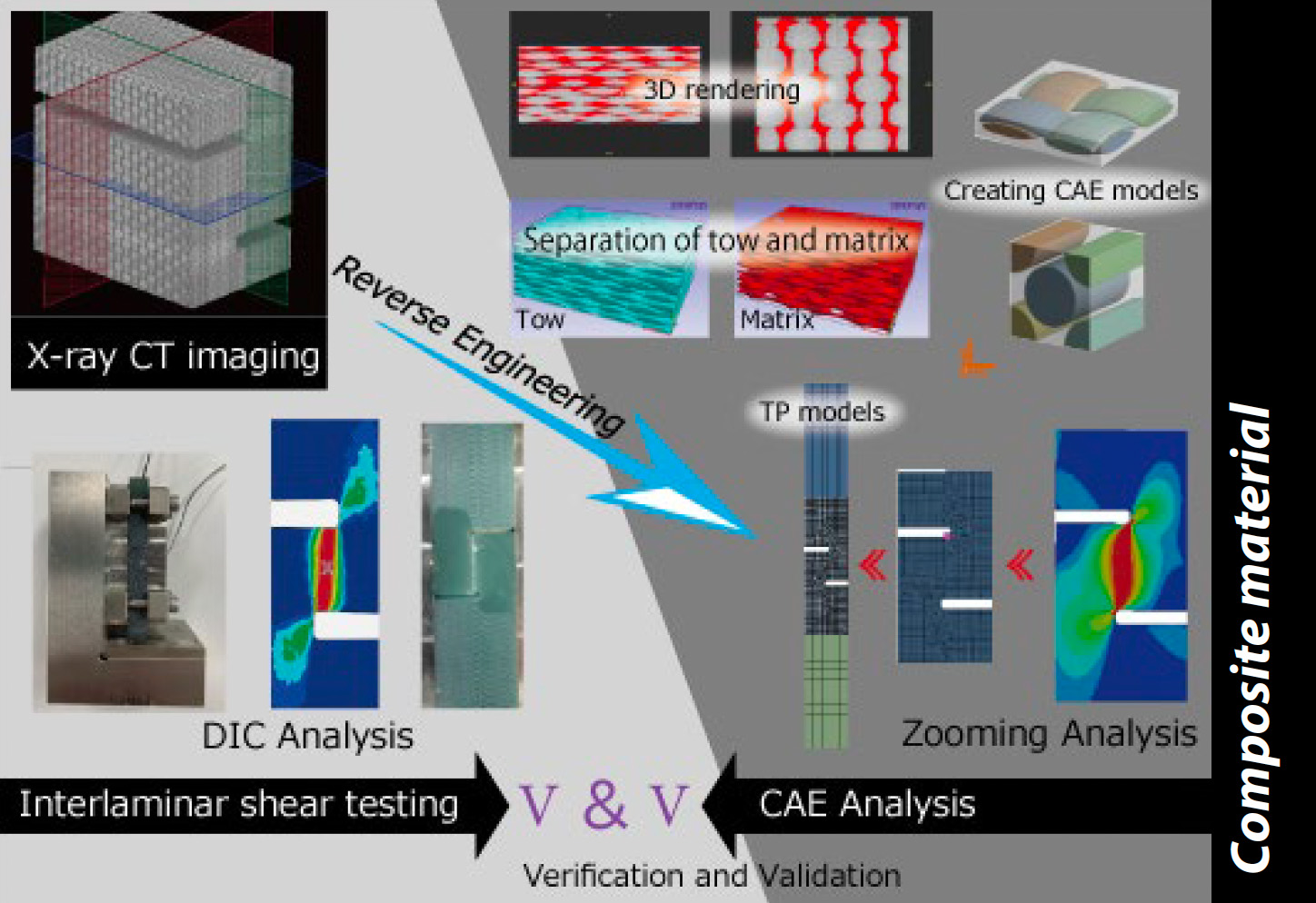
In den letzten Jahren gibt es eine starke Tendenz, neue Materialien aktiv zu nutzen, um die Leistung von Produkten zu verbessern, und es werden nach und nach neue Verbundwerkstoffe auf den Markt gebracht. Die Vielseitigkeit der Homogenisierungsmethode macht sie zum geeignetsten Ansatz für die Trends in diesem Materialmarkt. Einzelheiten zur Homogenisierungsmethode finden Sie in der vorliegenden Application Note Nr. 58 (11). Es ist wichtig, an dieser Stelle zu betonen, dass die Homogenisierungsmethode auch Eingangsinformationen wie die Form der Mikrostruktur und die Materialeigenschaften der einzelnen Fasern und Harze benötigt, um Simulationen durchzuführen. Mit anderen Worten: Das Problem, physikalische Eigenschaften zu erhalten, kann nicht allein durch Analysetechnik gelöst werden, sondern die Eigenschaften von Verbundwerkstoffen können nur durch eine Kombination von Messung und Analyse bestimmt werden.
In der Application Note Nr. 58 wurden Beispiele für die Überprüfung der einachsigen Zugeigenschaften von Verbundwerkstoffen durch eine Kombination aus Messung und Analyse vorgestellt. In diesem Artikel liegt der Schwerpunkt auf dem Scherverformungsmodus, und es wird ein Forschungsbeispiel vorgestellt, das Messung und Analyse kombiniert. Zunächst wurde ein analytisches Modell erstellt, das auf den Ergebnissen der Beobachtung der heterogenen mesoskaligen Struktur durch Röntgen-Computertomographie (CT) basiert, und die Eigenschaftswerte wurden durch eine Homogenisierungsanalyse vorhergesagt. Die Gültigkeit des Modells wurde durch den Vergleich der vorhergesagten Ergebnisse mit den tatsächlichen Ergebnissen für reine Scherung überprüft. Darüber hinaus wurde eine separate Analyse durchgeführt, bei der die durch die im Versuch verwendete Prüfvorrichtung (eine Vorrichtung gemäß JIS K 7092) auferlegten Zwangsbedingungen des Probekörpers mithilfe eines Reibungskoeffizienten reproduziert wurden. Die analytischen Ergebnisse wurden mit den experimentellen Ergebnissen verglichen, um die Gültigkeit der experimentellen Ergebnisse zu überprüfen.
Bestimmung der verschiedenen für die Erstellung des Modells erforderlichen Parameter
Bewertung der interlaminaren Schereigenschaften von GFK-Gewebe
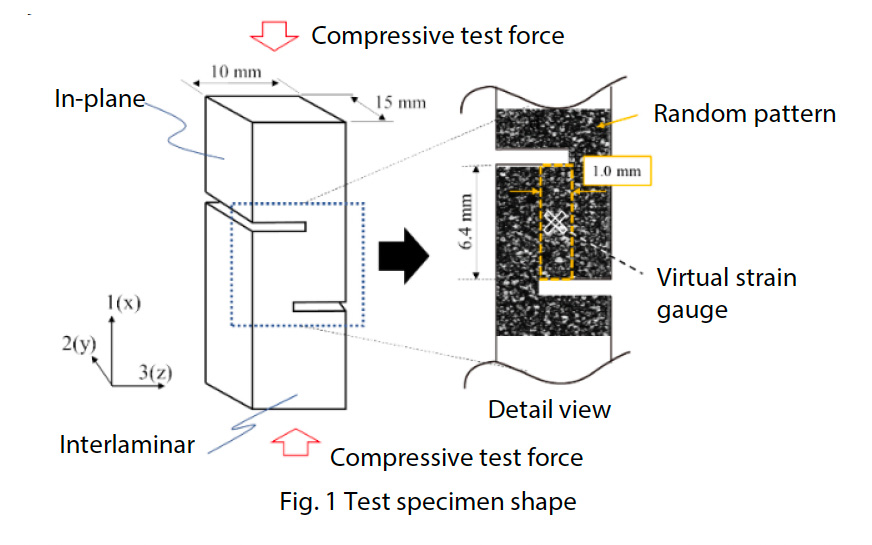
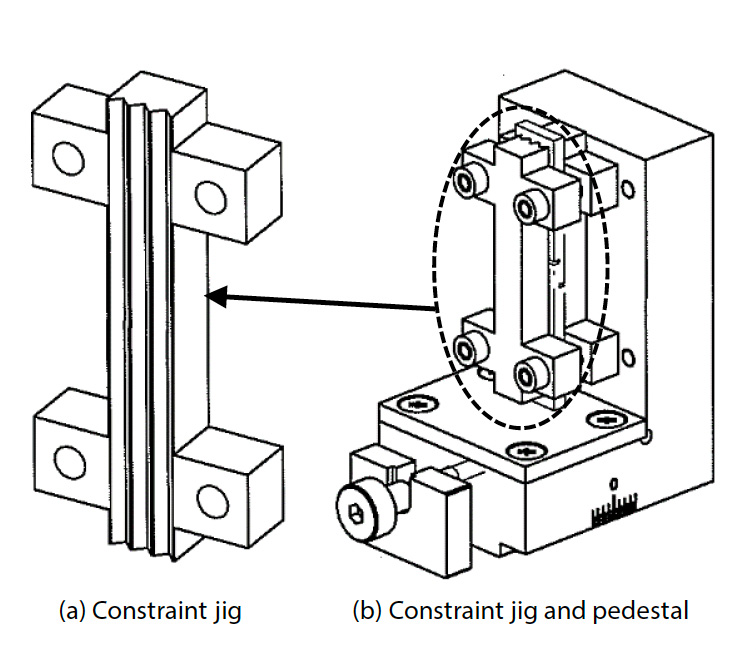
Wie in Abb. 1 dargestellt, wurde der Probekörper aus einer flachen GFK-Gewebeplatte mit einer Dicke von etwa 10 mm hergestellt. Die Gesamtlänge des Probekörpers betrug 80 mm, und um die Scherbelastung zwischen den eingekerbten Nuten zu konzentrieren, die einer Scherbelastung ausgesetzt sind, wurden die eingekerbten Nuten um 1 mm überlappt, um den Scherverformungsbereich gegenüber der in JIS K 7092 (5) spezifizierten Form zu erweitern, und die Dehnungsverteilung im Scherverformungsbereich wurde gleichmäßig gestaltet (4). Die Spaltbreite der Kerbnuten wurde auf 1 mm festgelegt. Auf die Oberfläche des Probekörpers wurde ein Zufallsmuster aufgebracht, indem ein schwarzes und anschließend ein weißes Spray aufgetragen wurde. Der Probekörper wurde in ein System für interlaminare Scherprüfungen eingespannt, das aus einer JIS K 7092-konformen Vorrichtung und einem Druckbrett mit einem Mechanismus zur Einstellung der Parallelität bestand. 
γXZ=|ε_ (+45) |+|ε_ (-45) | (1)
|ε_ (+45) | : Absoluter Wert der Dehnung, der sich aus dem Ausgang des virtuellen Dehnungsmessstreifens ergibt, der bei + 45° installiert ist
|ε_ (-45) | : Absoluter Wert der Dehnung, der aus dem Ausgang des bei -45° installierten virtuellen Dehnungsmessers gewonnen wird
Die Nenn-Schubspannung τXZ wurde aus Gleichung (2) berechnet.
τXZ= F/ab (2)
F: Prüfkraft (N), a: Abstand zwischen gekerbten Rillen (6,4 mm), b: Probenbreite (15 mm)
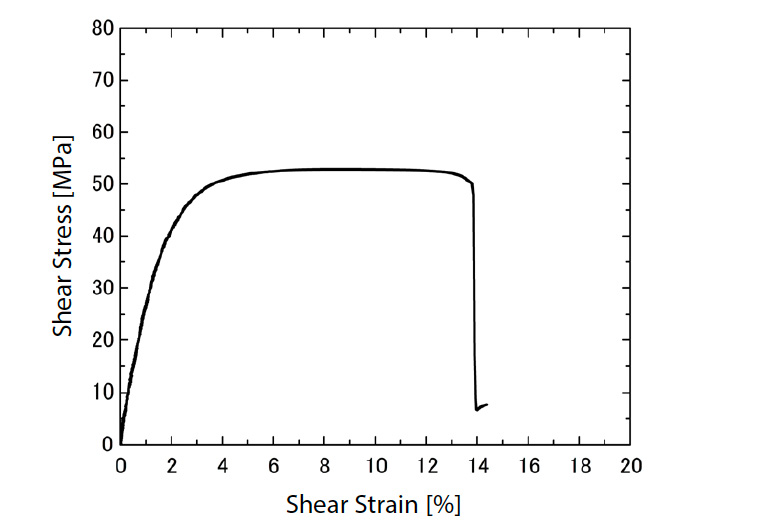
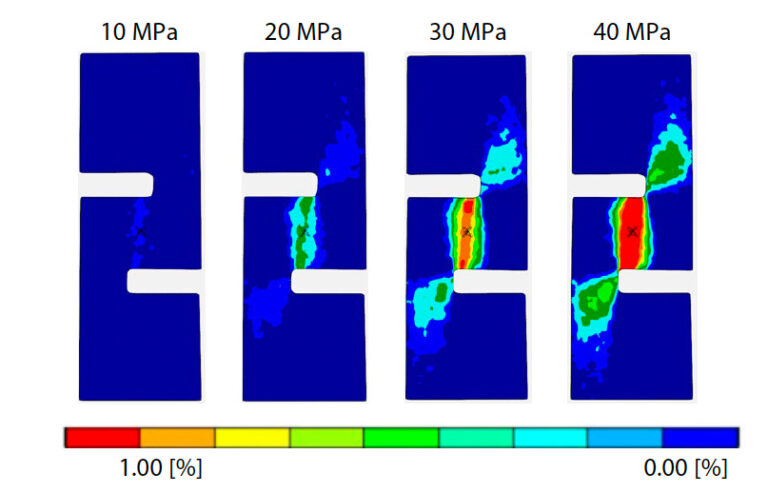
Abb. 5 zeigt das interlaminare Scherspannungs-Dehnungs-Diagramm des glatten gewebten GFK, das in diesem Test erhalten wurde. Die Beziehung zwischen Spannung und Dehnung von glattem GFK-Gewebe ist bis zu einer Scherspannung von etwa 30 MPa linear, danach wird sie jedoch nichtlinear und gibt bei etwa 50 MPa nach. Wie bereits erwähnt, hat GFK-Gewebe eine Struktur, bei der mit Harz imprägniertes Glasfasergewebe laminiert ist. Daher ist das GFK-Gewebe in der interlaminaren Richtung reich an Harz, und es wird angenommen, dass die Nichtlinearität aufgrund der Duktilitätseigenschaften des Harzes auftritt. Abb. 6 zeigt Konturdiagramme der interlaminaren Scherdehnung aus den Ergebnissen der DIC-Analyse bei 10 bis 40 MPa. Die interlaminare Scherdehnung ist von Beginn der Prüfung an gleichmäßig und breit zwischen den Kerben des GFK-Gewebes verteilt, und diese Tendenz bleibt auch dann erhalten, wenn die auf den Probekörper aufgebrachte Last steigt. Aus der Beziehung mit der Spannung im linearen Anfangsbereich, 0,1 bis 0,3 % Dehnung in Abb. 5, wurde der interlaminare Schermodul durch die Methode der kleinsten Quadrate berechnet und betrug 2546,1 MPa.
Bewertung der Probeneinspannbedingungen durch Messung des Reibungskoeffizienten
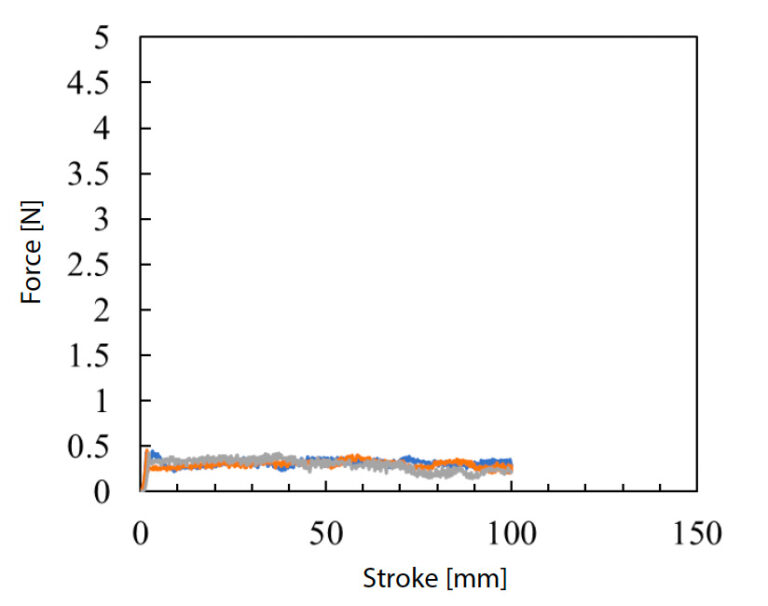
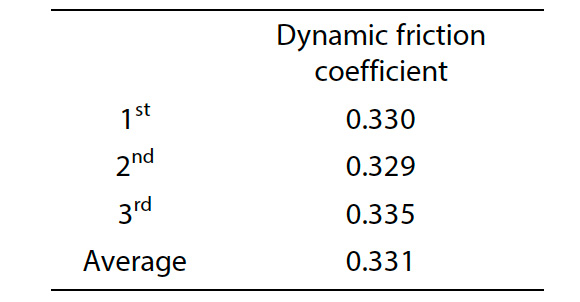
Die Belastungsbedingungen der im interlaminaren Scherversuch verwendeten Probekörper wurden durch Messung des Reibungskoeffizienten mit der Präzisions-Universalprüfmaschine Autograph AGX-5NV und dem Reibungskoeffizienten-Messgerät geschätzt. Abb. 7 zeigt die Prüfung. Bei der Durchführung der Prüfung wurde eine flache Platte aus GFK-Gewebe mit einer Dicke von 10 mm auf den Prüfraum der Prüfmaschine gelegt, nachdem die gekerbte Probe ausgeschnitten worden war, und eine Spannvorrichtung wurde auf der flachen Platte installiert, so dass die Kontaktfläche der Probe sie berühren konnte. Die Prüfgeschwindigkeit wurde auf 100 mm/min eingestellt, und die Prüfkraftdaten wurden ermittelt, wenn der Hub der Prüfmaschine 100 mm betrug. Um die Reproduzierbarkeit der gewonnenen Daten zu bestätigen, wurden drei Tests durchgeführt. Der dynamische Reibungskoeffizient für die Anwendung in der CAE-Analyse wurde aus den durchschnittlichen Prüfkraftdaten für einen Hub von 20 bis 60 mm berechnet, die mit einer stabilen Prüfkraft und dem Gewicht der Vorrichtung ermittelt wurden. Abb. 8 zeigt das Prüfkraft-Hub-Diagramm, und Tabelle 1 zeigt die Berechnungsergebnisse des dynamischen Reibungskoeffizienten. Aus den obigen Ergebnissen geht hervor, dass der Koeffizient der dynamischen Reibung, der an der Kontaktfläche zwischen der Probe und der Spannvorrichtung entsteht, 0,33 beträgt.
Erfassung von Daten über die Form gekerbter Proben mit einem Röntgen-CT-System
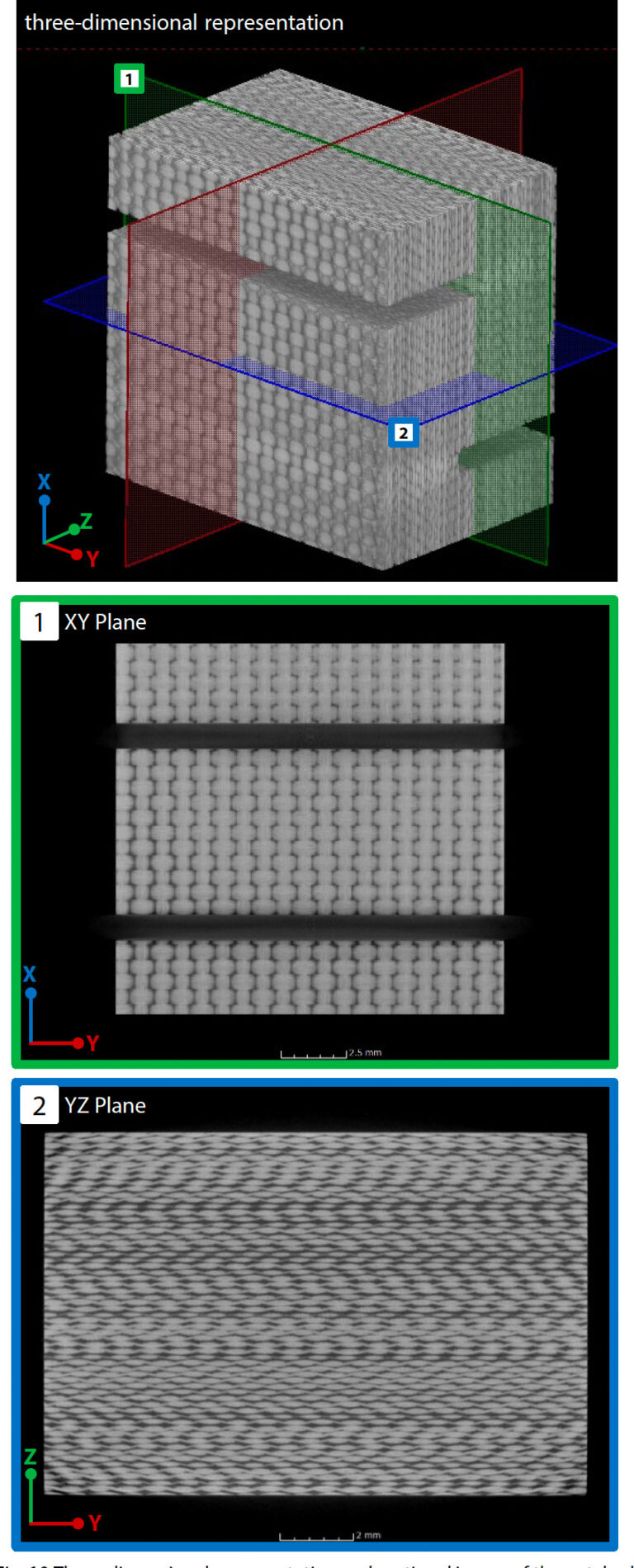
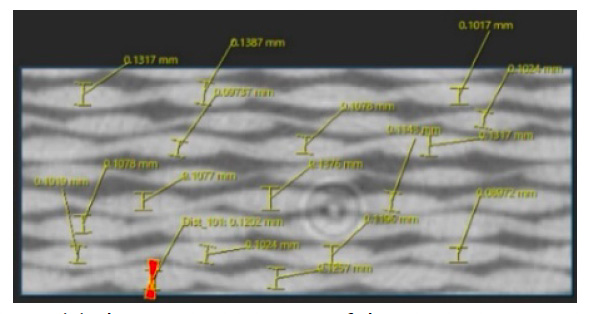
Mit dem in Abb. 9 gezeigten Mikrofokus-Röntgen-CT-System inspXio™ SMX™-225 CT FPD HR Plus wurden Querschnittsbilder der gekerbten Probe aufgenommen, um die Form des analytischen Modells zu bestimmen. Unter den in Tabelle 2 aufgeführten Bedingungen wurden CT-Bilder in der Nähe der Kerbnut des Prüfkörpers aufgenommen und mehrere hundert Querschnittsbilder im DICOM-Format (Digital Imaging and Communications in Medicine) ausgegeben. Abb. 10 zeigt Querschnittsbilder und eine dreidimensionale Darstellung, die mit einer dreidimensionalen Bildanalysesoftware auf der Grundlage der Querschnittsbilder erstellt wurde. In einem Querschnittsbild erscheinen Bereiche mit hoher Dichte und hoher Röntgenabsorption weiß und Bereiche mit geringer Dichte und niedriger Röntgenabsorption schwarz. Die Bildverarbeitung wurde durchgeführt, um aus dem Querschnittsbild ein Modell für die Finite-Elemente-Analyse zu erstellen. Durch die Analyse der mittels CT-Bildgebung gewonnenen Querschnittsbilder mit Simpleware™ von Synopsys wurden die für die Erstellung des Analysemodells erforderlichen Formparameter der Mikrostruktur ermittelt. Für das zu untersuchende GFK-Gewebe sind die Faktoren, die die Materialeigenschaften beeinflussen, der Volumengehalt und die Querschnittsform des Wergs (ein Bündel von mehreren hundert bis 1000 in einer Richtung angeordneten Fasern) sowie der Abstand zwischen benachbarten Faserbündeln. Der Gehalt an Monofilamenten im Inneren des Wergs wirkt sich ebenfalls auf die Materialeigenschaften aus, aber in diesem Analysebild war es nicht möglich, selbst im feinen Bereich im Inneren des Wergs einen klaren Kontrast zu erhalten, so dass dieser durch Abgleich mit dem Montageergebnis bestimmt wurde. Einzelheiten werden in Abschnitt 3 beschrieben. Diese Formparameter sind nicht einheitlich über das gesamte Material verteilt und weisen Schwankungen auf. Daher wurde im Bildanalysewerkzeug ein relativ breiter Bereich, der mehrere Faserbündel umfasst, gemessen, und der Durchschnittswert wurde als Form des Analysemodells angenommen.
Modellbildung
Identifizierung von Formparametern
Abb. 11 zeigt den mit Simpleware gemessenen Volumenanteil des Wergs. Die Trennung zwischen dem Wergbereich und dem Matrixbereich erfolgte durch Binarisierung des aus dem Röntgen-CT gewonnenen Graustufenbildes mit geeigneten Schwellenwerten. Der Volumenanteil wurde durch Messung des Volumens der einzelnen getrennten Bereiche bestimmt.
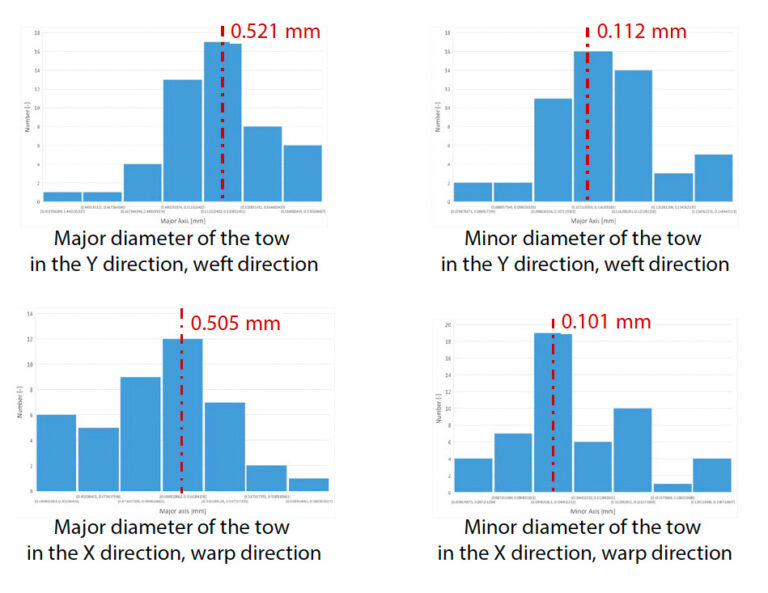
Abb. 12 zeigt die Querschnittsform des Tows und den gemessenen Abstand zwischen den Tows. Es wurde angenommen, dass das Kabel einen elliptischen Querschnitt hat, und es wurden der große und der kleine Durchmesser gemessen. Es wurden 49 Schleppnetze nach dem Zufallsprinzip ausgewählt. Abb. 12 zeigt das Ergebnis der Erstellung eines Histogramms mit 7 Bins durch Anwendung des Quadratwurzel-Theorems auf die Anzahl der Messpunkte für jeden gemessenen Formparameter. Da es keine Tendenz gab, dass alle Formparameter eindeutig mit einer allgemeinen statistischen Funktion wie der Gauß-Verteilung übereinstimmen, wurde der Durchschnittswert des Bins mit der höchsten Wahrscheinlichkeit als Formparameter verwendet. Dieses Ergebnis zeigt, dass die Form des Abschleppens in X- und Y-Richtung deutlich unterschiedlich ist. Da es jedoch im Allgemeinen äußerst selten ist, ein Produkt unter Berücksichtigung dieser richtungsabhängigen Mikrostrukturen zu entwerfen, wurde dieses Mal ein weiterer Mittelwert der Durchschnittswerte in beiden Richtungen gleichermaßen auf das Werg angewendet.
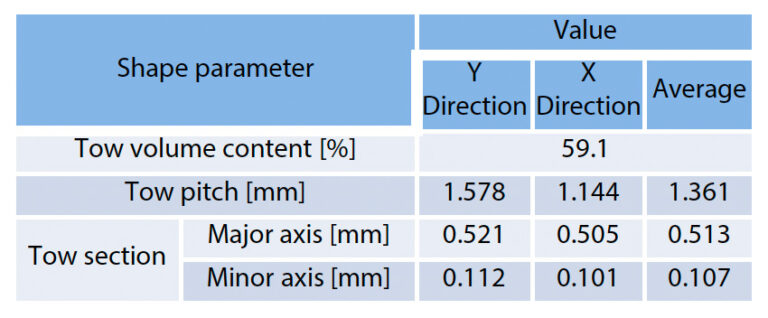
Ein Messbild des Abstandes zwischen benachbarten Tows ist ebenfalls in Abb. 12 (c) dargestellt. Dieser Formparameter wurde aus einem Out-of-Plane-Bild gemessen. Die Grenze zwischen den Bereichen, die nicht durch das senkrechte Kabel verdeckt werden, und den Bereichen, die durch das senkrechte Kabel verdeckt werden, ist reich an Kunststoff und erscheint daher dunkel. Infolgedessen erscheinen die Bereiche, die nicht von orthogonalen Schlepps verdeckt werden, und die Bereiche, die von orthogonalen Schlepps verdeckt werden, als separate rechteckige Formen. Der Schleppabstand wurde als der Abstand zwischen den Mittelpunkten dieses Rechtecks definiert. Wie bei der Querschnittsform des Schlepps wurde auch der Abstand zwischen 49 Schlepps gemessen. Für den Abstand zwischen den Tauen wurde eine Tendenz zur Abhängigkeit von der vertikalen und der vertikalen Faserrichtung in (c) in derselben Abbildung beobachtet, und der Durchschnittswert wurde dann auf das Analysemodell angewandt. Tabelle 3 und Abb. 13 geben einen Überblick über die endgültig ermittelten Formparameter und die für den numerischen Test tatsächlich erstellten Analysemodelle.
Optimierung der Formparameter
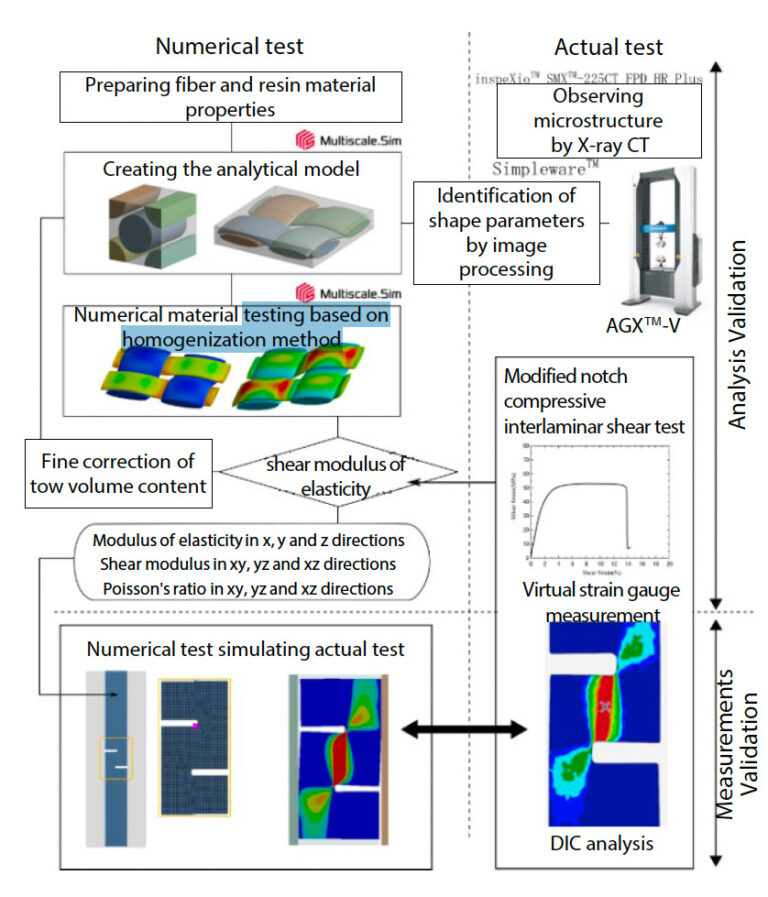
Endlosfaserverstärkte Materialien, wie das in dieser Analyse verwendete Gewebe, neigen zu extrem starker Anisotropie. Analytische Methoden, die auf der Homogenisierungsmethode (10) beruhen, sind wirksam für die analytische Vorhersage von Materialeigenschaften, die das anisotrope Verhalten charakterisieren. Die Homogenisierungsmethode bietet einen analytischen Ansatz zur Bewertung der offensichtlichen Materialreaktion und letztlich zur Ermittlung der Materialeigenschaften durch die Durchführung eines numerischen Tests. Durch einfaches Messen der Materialeigenschaften einzelner Fasern und Harze (und der Eigenschaften der Materialgrenzfläche, wenn diese berücksichtigt werden sollen) oder durch Beschaffung aus einer Datenbank usw. können anisotropes Materialverhalten und Materialeigenschaften für alle Arten von Verstärkungen auf der Grundlage ihrer heterogenen Mikrostruktur ermittelt werden. Einzelheiten zu dieser Analysemethode finden Sie in der Application Note Nr. 58 (11). Der Gesamtablauf der Analyse ist in Abb. 14 dargestellt. Es wurde versucht, die Gültigkeit sowohl der Analyse als auch der Messung zu überprüfen. Die analytische Validierung wurde durch die oben beschriebene Homogenisierungsanalyse durchgeführt. Die erforderlichen Informationen waren die Form der Mikrostruktur und die Eigenschaften der Materialien, aus denen sie zusammengesetzt war. Die spezifischen Werte der für die Modellierung der Mikrostruktur erforderlichen Formparameter wurden ermittelt, indem die von der Röntgen-CT beobachteten Daten einer Bildverarbeitung unterzogen wurden, wie in Abschnitt 2-3 beschrieben.
Validierung der Prüfmethode
Um die Gültigkeit der eigentlichen Prüfmethode zu überprüfen, wurde eine Analyse mit der gleichen Form und den gleichen Randbedingungen wie bei der Prüfung durchgeführt. Die Materialeigenschaften des in diesem Analysemodell verwendeten Glattgewebe-Materials wurden in der Verifizierungsphase der Analyse ermittelt. Durch den Vergleich der durch die Analyse erhaltenen Scherdehnungsverteilung in der Probe mit dem durch die DIC-Analyse gemessenen Ergebnis wurde bestätigt, dass das analytische Ergebnis gut mit dem tatsächlichen Prüfergebnis übereinstimmt. Gleichzeitig wurde versucht, die Bedingungen zu quantifizieren, die sich auf die Prüfergebnisse auswirken, indem der Reibungskoeffizient zwischen der Spannvorrichtung und der Probe mit den analytischen Ergebnissen verglichen wurde, die durch eine virtuelle Änderung der Spannkraft der Spannvorrichtung erzielt wurden.
Analyse-Methode
Zunächst wurden die orthotropen Materialeigenschaften von GFK-Gewebe durch Homogenisierungsanalyse berechnet. Abb. 15 zeigt die Festkörper- und Finite-Elemente-Modelle des in der Analyse verwendeten GFK-Gewebes. Wie bereits erwähnt, wurden die mesoskaligen Gewebestrukturen durch Bildverarbeitung der Ergebnisse der Röntgen-CT identifiziert. Das mesoskalige Modell geht davon aus, dass der Wergbereich homogen ist. In Wirklichkeit weist das Material eine inhomogene Struktur auf, die aus in eine Richtung ausgerichteten Faserbündeln besteht, so dass es notwendig ist, anisotrope Materialeigenschaften bereitzustellen, die die mikroskopische Struktur widerspiegeln. Daher wurde das in Abb. (a-2) gezeigte Modell und Abb. (b-2) gezeigte Modell wurde daher für die Faserbündel im Wergbereich erstellt, und es wurde eine separate Homogenisierungsanalyse durchgeführt, um die physikalischen Eigenschaften zu erhalten. Die Materialien, aus denen der Verbundwerkstoff besteht, sind E-Glas (Elastizitätsmodul: 72,5 GPa, Poissonzahl: 0,2) für die Fasern und Epoxidharz (Elastizitätsmodul: 3,5 GPa, Poissonzahl: 0,35) für die Harze. Es wurde davon ausgegangen, dass diese beiden Eigenschaften elastisch sind, und es wurde auf die Werte in der vom Analysetool bereitgestellten Materialdatenbank zurückgegriffen. In der Homogenisierungsanalyse wurden alle Materialeigenschaften, die die orthotropen Eigenschaften der GFK-Gewebe charakterisieren, durch die Durchführung numerischer Tests ermittelt, die ideale einachsige Zug- und interlaminare Scherbelastungen für diese Modelle simulierten. Die Materialeigenschaften bestanden aus 9 Arten von physikalischen Eigenschaften: dem Längselastizitätsmodul, der Poissonzahl und dem Scherelastizitätsmodul in 3 Richtungen. Abb. 16 zeigt das analytische Modell, das zur Überprüfung der experimentellen Seite durchgeführt wurde. Das Modell bestand aus einem GFK-Probekörper und einer Einspannvorrichtung, die den Probekörper in Dickenrichtung hält. Die Druckbelastungen und Druckspannungen auf die Proben und die Einspannvorrichtung wurden direkt auf diesen Teilflächen definiert, und andere Geometrien (Schraubenlöcher der Einspannvorrichtung, Einspannvorrichtung zur Unterstützung der Probe von der Ober- und Unterseite der Figur usw.) wurden nicht berücksichtigt. rigoros modelliert. Konkret wurde die Unterseite der Probe in Abb. 16 mit einer vollständigen Verschiebungsbeschränkung und die Oberseite mit einer Druckspannung von 30 MPa definiert. In der tatsächlichen Prüfung wurde über das auf die Spannvorrichtung ausgeübte Drehmoment eine Schubkraft in Richtung der Außenebene aufgebracht, aber in der Analyse wurde die Verschiebung der Spannvorrichtung auf Null beschränkt. Darüber hinaus wurde auch der Fall analysiert, in dem die Vorrichtung nicht installiert war. Es wurde erwartet, dass die Dehnungsverteilung in der Nähe der GFK-Kerbe komplex sein würde, aber in dem Bereich, der weit genug von der Kerbe entfernt ist, sollte die Spannungs- und Dehnungsverteilung fast gleichmäßig sein. Daher wurde das GFK-Teil in den Bereich nahe der Kerbe und die anderen Bereiche unterteilt, und das Netz wurde nur in der Nähe der Kerbe feinmaschig ausgelegt. Zwischen zwei unterschiedlich grobmaschigen Teilen bestand ein diskontinuierliches Netz, aber durch die Definition einer Mehrpunktbeschränkung (MPC) an der Grenzfläche wurde ein realistischer Befestigungszustand reproduziert. Was das Materialverhalten betrifft, so wurden dem GFK-Teil die Materialeigenschaften aus der oben dargestellten Homogenisierungsanalyse zugewiesen, und es wurde angenommen, dass die Vorrichtung starr und nicht verformbar ist. Der Reibungskoeffizient zwischen dem GFK-Gewebe und der Spannvorrichtung wurde in 3 Mustern analysiert, 0,0, 0,3 und 0,4, um die Auswirkungen auf die Testergebnisse zu bestätigen. Aus den Daten der Analyseergebnisse wurden die interlaminare Scherdehnungsverteilung sowie die Scherdehnungs- und Scherspannungswerte in der Mitte des Probekörpers ermittelt. Die Gültigkeit der Versuchsbedingungen wurde durch den Vergleich dieser Ergebnisse mit der gemessenen Scherdehnungsverteilung, die mit der DIC-Analyse ermittelt wurde, und der gemessenen Scherdehnung in der Mitte der Probe, die mit dem virtuellen Dehnungsmessstreifen ermittelt wurde, überprüft. Bei diesem Versuch wird die Druckspannung von 30 MPa, die auf den oberen Teil der Probe einwirkt, im Idealfall genauso übertragen wie die Scherspannung in der Mitte des Probekörpers. Die Scherspannung in den Analyseergebnissen wurde beobachtet, um festzustellen, ob dieser Idealzustand erreicht wurde.CAE-Analyseergebnisse
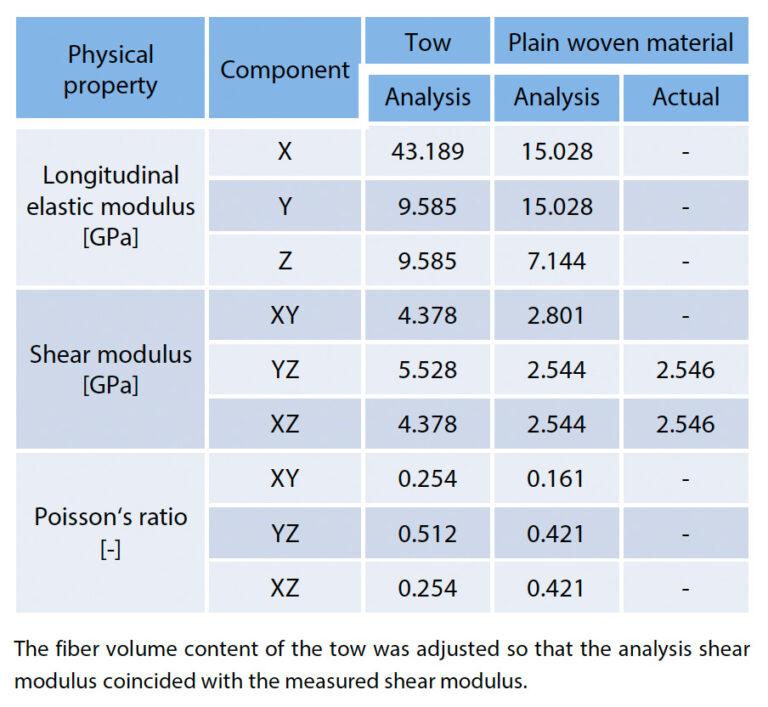
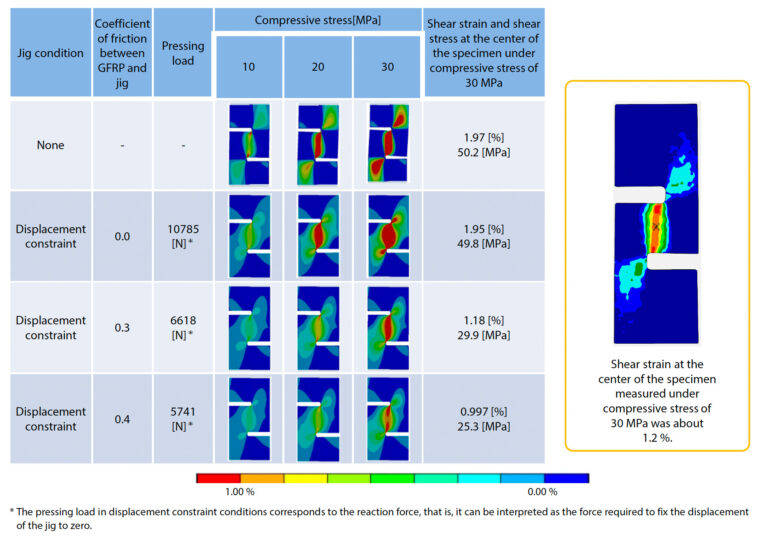
Zunächst wurde eine Homogenisierungsanalyse für das in Abb. 16 gezeigte analytische Modell durchgeführt, und die Ergebnisse der Auswertung der orthotropen Elastizitätsmodule des Wergbereichs und des gesamten Flachgewebes sind in Tabelle 4 dargestellt. Da die Schersteifigkeit des Glattgewebes im Versuch bewertet wurde, wurde der Faservolumengehalt des Tow-Bereichs in der Analyse so angepasst, dass der Analyseschermodul mit dem gemessenen Schermodul übereinstimmt. Der schließlich durch inverse Schätzung ermittelte Faservolumengehalt des Tow-Bereichs lag bei etwa 57,27 %. Dieser Wert unterscheidet sich nicht wesentlich von anderen Studien, die mit dem SEM durchgeführt wurden, und wird als angemessen angesehen. Tabelle 5 fasst die Ergebnisse der einzelnen Fallstudien zusammen, bei denen das optimierte Modell verwendet wurde, um das Vorhandensein oder Nichtvorhandensein einer Einspannvorrichtung zu variieren und den Reibungskoeffizienten zwischen der Einspannvorrichtung und der Probe zu verändern. Die Ergebnisse der gemessenen Scherdehnungsverteilung aus der DIC-Analyse sind ebenfalls rechts und außen in Tabelle 5 dargestellt. Unter allen Bedingungen ist zu erkennen, dass sich die Scherdehnung in der Nähe der Mitte der zwischen den beiden Kerben eingebetteten Probe konzentriert. Daraus lässt sich jedoch ableiten, dass die Verformung der Probe unterschiedlich ist, da die Dehnungsverteilung von den Spannungsbedingungen in dem Bereich abhängt, der etwas von der Mitte entfernt ist, sowie auf der Randseite der beiden Kerben. Wenn die Spannvorrichtung nicht installiert ist, ist eine hohe Dehnung in der gleichen Größenordnung wie in der Mitte der Probe festzustellen, die sich von der Kerbe bis zum Rand erstreckt. Dies könnte auf eine Verformung der Probe durch Knicken außerhalb der Ebene zurückzuführen sein. Die Ergebnisse zeigen auch, dass die Scherspannung in der Mitte der Probe größer ist als der äußere Druck, was darauf hindeutet, dass keine genaue Scherverformung außerhalb der Ebene erreicht werden kann. Unter der Bedingung, dass die feste Spannvorrichtung angebracht ist, ist der Bereich hoher Scherspannungen an der Stirnseite der Kerbe klein, so dass die Knickverformung unterdrückt wird. Es wurde bestätigt, dass der Grad der Unterdrückung umso ausgeprägter ist, je größer der Reibungskoeffizient zwischen dem GFK-Gewebe und der Einspannvorrichtung ist. Als der Reibungskoeffizient auf 0,4 anstieg, wurde die Spannung in der Mitte des Probekörpers jedoch kleiner als der äußere Druck. Es wird davon ausgegangen, dass dies darauf zurückzuführen ist, dass die Energie des Außendrucks durch die Reibungswiderstandskraft in einem nicht zu vernachlässigenden Maße verloren geht. In einem realen Versuch kann der Reibungskoeffizient nicht kontrolliert werden, so dass eine angemessene Presskraft aufgebracht werden muss, um die Verformung in der Ebene nicht zu sehr zu unterdrücken und gleichzeitig das Ausknicken der Probe außerhalb der Ebene zu verhindern.
In dem in Abschnitt 2-2 beschriebenen Versuch wurde der Reibungskoeffizient zwischen den Materialien mit etwa 0,3 bestätigt. Unter diesen Bedingungen ist die Scherspannung in der Mitte der Probe gleich dem Außendruck, was bedeutet, dass ideale Scherbedingungen erreicht werden.
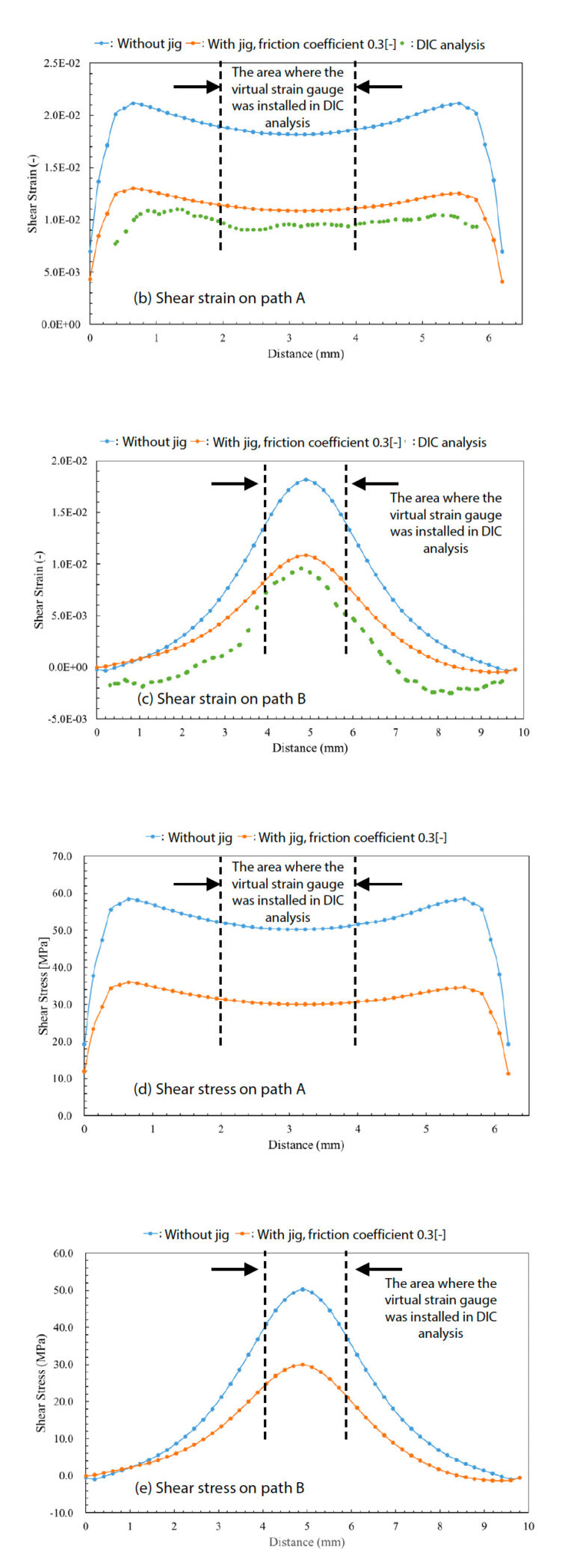
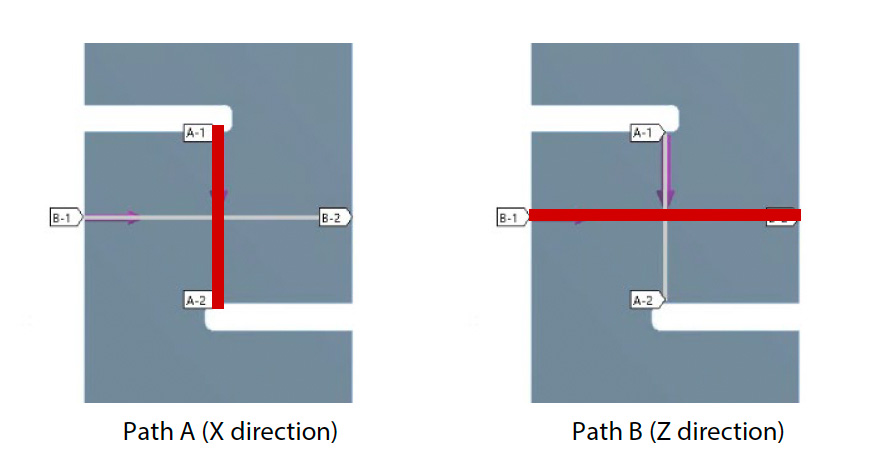
Um schließlich die Scherdehnungsverteilung in der Nähe der Kerben genauer zu betrachten, wurden die Ergebnisse der Scherdehnung und der Scherspannung über die beiden in Abb. 17 (a) dargestellten Pfade aufgetragen. Die Ergebnisse sind in Abb. (b) bis (e) dargestellt. Die Mitte der Probe entspricht einem Abstand von 3,2 mm in Pfad A und 5,0 mm in Pfad B. In der DIC-Analyse befindet sich der Bereich, in dem der virtuelle Dehnungsmessstreifen installiert wurde, in der Nähe der Mitte. Für eine genaue interlaminare Scherprüfung wird erwartet, dass sich der zentrale Teil der Probe in einem idealen Schermodus befindet, aber es ist auch wünschenswert, dass ähnliche Bedingungen in einem weiten Bereich in der Umgebung bestehen. Insbesondere bei der Messung lokaler Dehnungswerte mit einem Dehnungsmessstreifen ist es wünschenswert, einen konstanten Wert innerhalb eines Messbereichs von etwa 2 mm x 2 mm zu erhalten.
Unter den in Abb. 17 (b) und (c) dargestellten Bedingungen, in denen die Einspannvorrichtung angebracht ist, wird dies fast erreicht, und es wird erwartet, dass die interlaminaren Schereigenschaften der Probe mit einer gewissen Genauigkeit gemessen werden können. Andererseits ist in dem Fall, in dem die Spannvorrichtung nicht angebracht ist, aufgrund des Knickens außerhalb der Ebene die mittlere Scherdehnung im Vergleich zur Messung ungewöhnlich groß, und das Ergebnis auf Pfad A ist bemerkenswert konvex nach unten, wie in Abb. 17 (b) gezeigt.
Die Verteilung der Scherspannung wurde ebenfalls überprüft, und es wurde festgestellt, dass die in Abb. 17 (d) gezeigte Scherspannung unter der Bedingung, dass die Spannvorrichtung platziert wurde, bis zu einem gewissen Grad auf dem Pfad A breit verteilt war, ähnlich wie die Scherdehnung. Darüber hinaus wurde bestätigt, dass der virtuelle Dehnungsmessstreifen, der in der DIC-Analyse verwendet wurde, in dem Bereich, in dem der virtuelle Dehnungsmessstreifen auf der Bahn B installiert war, breit verteilt war, und zwar in der Nähe der Mitte zwischen den gekerbten Nuten, was einem Abstand von 2 bis 4 mm auf der Bahn B entspricht. Bei der Prüfung gibt es keine andere Methode zur Bewertung der Spannung als die Berechnung der nominalen Scherspannung durch Division der in der Kraftmessdose der Prüfmaschine gemessenen Prüfkraft durch die Querschnittsfläche der Probe, wie in Gleichung (2) in Abschnitt 2-1 dargestellt. In den in Abb. 17(d) gezeigten Ergebnissen gibt es keine Spannungskonzentration in der Nähe der Kerbe in der Probe, und die gleichmäßige Spannungsverteilung über das Kerbenintervall von 6,4 mm kann nur durch die CAE-Analyse verifiziert werden. Die Ergebnisse der CAE-Analyse zeigten keine signifikante lokale Spannungskonzentration, was beweist, dass die in der Prüfung angewandten Prüfmethoden und -geometrien für die Bewertung der nominalen Scherspannung sowie der linearen und nichtlinearen Dehnung nützlich sind.
Diese Ergebnisse zeigen, dass der interlaminare Scherversuch reproduziert werden kann, indem die Vorrichtung außerhalb der Ebene der Probe platziert und mit einer moderaten Last unterstützt wird, die das tangentiale Gleiten der Materialschnittstelle zwischen Werkzeug und Probe nicht beeinträchtigt, aber das normale Knicken unterdrückt.
Zusammenfassung
In diesem Beitrag wurde ein Fall vorgestellt, in dem die interlaminare Schercharakteristik von GFK-Geweben durch die interlaminare Scherprüfmethode unter Verwendung der modifizierten Kerbdruckmethode sowohl aus der experimentellen DIC-Analyse als auch aus der CAE-Analyse bewertet wurde.
Das CAE-Analysemodell wurde erstellt, indem die Randbedingungen zwischen der Probe und der Einspannvorrichtung unter Berücksichtigung des Reibungskoeffizienten festgelegt wurden. Die Ergebnisse der DIC-Analyse und der CAE-Analyse waren in den folgenden drei Punkten zwischen den gekerbten Nuten der Probe nahezu identisch.
1. Konturdiagramm der Scherdehnungsverteilung
2. Form der Scherdehnungsverteilung in X-Richtung
3. Form der Scherdehnungsverteilung in Z-Richtung
Darüber hinaus war die durch die CAE-Analyse berechnete Spannungsverteilung zwischen den Kerbnuten breit und gleichmäßig, und es wurde keine lokale Spannungskonzentration beobachtet.
Die Methode der interlaminaren Scherprüfung mit der modifizierten Kerbverdichtung, die bei der eigentlichen Prüfung angewandt wurde, erwies sich nicht nur für die Ermittlung der linearen und nichtlinearen Dehnung, sondern auch für die Bewertung der nominellen Scherspannung als nützlich.
Referenzen
1) Pettersson KB, Neumeister JM. Ein Zugversuchsaufbau für den IDNS-Verbundwerkstoff-Schertest. Compos Part A Appl Sci Manuf 2006; 37 (2) : 229-42.2) Melin LN, Neumeister JM. Messung des konstitutiven Scherverhaltens von orthotropen Verbundwerkstoffen und Bewertung des modifizierten Iosipescu-Tests. Compos Struct 2006; 76 (1-2) : 106-15.
3) Julio F. Davalos a, Pizhong Qiao b, Vinod Ramayanam a, Luyang Shan b, Justin Robinso. Torsion von wabenförmigen FRP-Sandwichträgern mit einer sinusförmigen Kernkonfiguration. Compos Struct 2009; 88: 97-111
4) T. Murakami, T. Matsuo, T. Sumiyama, Experimental method and evaluation for interlaminar shear properties of randomly oriented strand thermoplastic composites based on modified double-notch specimen and two dimensional digital image correlation. J. Compos. Mater., in press, https://doi.org/10.1177/0021998320967719 (2020).
5) JIS K 7092. Prüfverfahren für die interlaminare Scherfestigkeit von kohlenstofffaserverstärktem Kunststoff mit einer Doppelkerbprobe. In: JIS-Handbuch. Tokyo: Japanese Standard Association; 2010.
6) Bouette B, Cazeneuve C und Oytana C. Auswirkung der Dehnungsgeschwindigkeit auf die interlaminaren Schereigenschaften von Kohlenstoff/Epoxid-Verbundwerkstoffen. Compos Sci Technol 1992; 45: 313-321.
7) Website des Ministeriums für Wirtschaft, Handel und Industrie: https://www.meti.go.jp/policy/digital_transformation/index.html
8) J.D.Eshelby, The determination of the elastic field of an ellipsoidal inclusion and related problems, Proc. Roy. Soc. Lond, Vol.A241, pp.376- 396 (1957).
9) T. Mori, K. Tanaka, verage stress in matrix and average elastic energy of materials with misfitting inclusions, Acta Metallurgica, Vol.21, No.5, pp.571- 574 (1973).
10) Terada, K., Kato, J., Hirayama, N., Inugai, T. und Yamamoto, K., A method of two-scale analysis with micromacro decoupling scheme: application to hyperelastic composite materials, Computational Mechanics, Vol.52, pp.1199-1219 (2013).
11) Koji Yamamoto, Takashi Murakami, Satoshi Iguchi, Zen Miyazaki Anwendungshinweis Nr.58 Verifizierung und Validierung (V&V) von Simulationsergebnissen einachsiger Zugversuche an Verbundwerkstoffen: Fusion von tatsächlichen Messungen und Homogenisierungsanalyse https://www.shimadzu.com/an/sites/shimadzu.com.an/files/pim/pim_d ocument_file/applications/application_note/11055/jpi320003.pdf
12) https://www.cybernet.co.jp/ansys/product/lineup/multiscale/multiscale/
13) https://www.cybernet.co.jp/ansys/product/
Herunterladen
- ApAnwendung: Validierung der Anwendbarkeit der modifizierten Kerbdruckmethode für interlaminare Scherprüfungen
English 
German 
Czech 
Slovak 
Bulgarian 
Romanian 