Abstrakt
Zkoumali jsme použitelnost modifikované metody zkoušení vrubového tlaku v mezivrstvovém smyku, která je účinná pro získání mezivrstvových smykových vlastností termoplastických CFRP, na hladké tkané materiály GFRP, které jsou široce používány v průmyslu. Na základě výsledků pozorování mezoměřítkové struktury pomocí rentgenového CT byl vytvořen model analýzy CAE a byla provedena homogenizační analýza zaměřená na omezující podmínky zkušebního vzorku z hlediska koeficientu tření. Naměřené hodnoty a výsledky analýzy vykazovaly dobrou shodu.
Úvod
V posledních letech se plasty vyztužené skleněnými vlákny (GFRP), které mají vysokou měrnou pevnost a vynikající zpracovatelnost a tvarovatelnost, široce uplatňují na elektronických substrátech, lodích a vnějších částech automobilů a staly se nepostradatelným materiálem. GFRP, který je kompozitním materiálem, má anizotropii a vykazuje komplikované deformační a lomové chování v závislosti na směru hlavní osy působícího napětí: tah, tlak, ohyb, smyk v rovině, mezilamelový smyk a smyk mimo rovinu nebo jejich kombinace. Při navrhování výrobků s využitím počítačem podporovaného inženýrství (CAE) je silně zapotřebí zkušebních metod, které mohou vyhodnotit chování při poruše každé součásti zvlášť.
*1 Cybernet Systems Co., Ltd. Mechanical CAE Div.
*2 SHIMADZU CORPORATION
Desky s plošnými spoji pro elektronická zařízení se hojně používají pro desky s plošnými spoji typu 4 (FR4), které jsou vyrobeny ze skleněných vláken a epoxidové pryskyřice.
Důvodem intenzivního používání materiálu FR4 je skutečnost, že hladce tkaný materiál GFRP má vysoké elektroizolační vlastnosti a nehořlavost a že díky zpevňujícímu účinku skleněných vláken dochází jen k malým rozměrovým změnám povrchu vlivem tepla. Protože má však tento materiál vrstvenou strukturu, jsou vlákna orientována v rovině, ale mezi laminami není téměř žádná orientace vláken, což z něj činí strukturu bohatou na pryskyřici. Zatímco ve směru v rovině se tedy projevují vynikající mechanické vlastnosti, v mezilaminárním směru je výztužný účinek vláken slabý, takže převládají fyzikální vlastnosti matricové pryskyřice a očekává se nelineární chování v důsledku poddajnosti pryskyřice. Je důležité přesně pochopit smykové vlastnosti v mezilaminárním směru, aby bylo možné pomocí numerické simulace reprodukovat deformační chování, které je výrazně ovlivněno vlastnostmi matriční pryskyřice, jako je ohyb a odlupování.
Jako reprezentativní metody měření mezilamelových smykových vlastností kompozitů bylo navrženo několik zkušebních metod (1-3). U všech zkušebních metod je tvar přípravku komplikovaný a je obtížné vyrobit zkušební vzorek pro zkoušku mezilamelového smyku, protože velikost zkušebního vzorku musí být dlouhá vzhledem ke směru laminace kompozitního materiálu.
(4). Mimochodem, zkušební metoda pevnosti ve smyku v mezivrstvovém tahu pomocí vrubové komprese, která působí tlakovým zatížením na čelní plochu malého zkušebního vzorku a která byla přijata v normě JIS K 7092, je široce používána jako zkušební metoda, kterou lze snadno vyhodnotit pevnost ve smyku v mezivrstvovém tahu plastů vyztužených uhlíkovými vlákny (CFRP).
(5). Velikost zkušebního vzorku ve směru laminace potřebná pro tuto zkoušku je pouhých 3,5 až 6,5 mm, což umožňuje snadnou výrobu zkušebních vzorků s malým množstvím materiálu. Touto zkušební metodou však nelze získat smykovou deformaci, protože oblast, kde se koncentruje smyková deformace v mezivrstvovém materiálu, je velmi úzká.
Pokud však jde o metodu tlakové zkoušky termosetových CFRP, v předchozím výzkumu
(6) bylo výpočtem navrženo, že oblast mezilamelového smykového namáhání lze rozšířit zvětšením velikosti překrytí vrubových drážek. V posledních letech byly publikovány příklady modifikovaných zkoušek tlakového mezilamelového smyku se zářezy, při nichž lze oblast mezilamelové smykové deformace rozšířit prohloubením zářezové drážky zkušebního vzorku a k oblasti deformace lze připojit tenzometr
(4). Bylo zjištěno, že nelineární charakteristiky mezilamelového smyku lze získat přímo z vypočteného jmenovitého smykového napětí získaného vydělením tlakové zkušební síly získané ze zkušebního stroje smykovou plochou mezi vrubovými drážkami a naměřené deformace získané z tenzometru. Při této zkušební metodě byla k pozorování a vyhodnocení malých ploch použita digitální kamera synchronizovaná se zkušebním strojem a měření deformace bylo provedeno pomocí digitální obrazové korelační analýzy (DIC). Použitím DIC analýzy pro měření deformace bylo zjištěno, že lze snadno měřit interlaminární smykovou deformaci od malé deformace až po velkou deformaci bez obav z poklesu nebo mezí měření během měření tenzometrem. V tomto článku zkoumáme, zda je modifikovaná metoda vrubové tlakové zkoušky, která je účinná při získávání mezilamelových smykových vlastností termoplastického CFRP, použitelná pro prostý tkaný GFRP, což je materiál vyztužený nekonečnými vlákny, který se široce používá v průmyslu.
Na druhou stranu, v reakci na snižování různých nákladů spojených s výrobou prototypů a nedávné hnutí na podporu digitální transformace (7) spojené s problémem nových koronavirů, nabývá na významu snaha nahradit část skutečných testů numerickou simulací (CAE analýza). Vstupní informace potřebné k dosažení analýzy CAE lze obecně rozdělit do tří typů: modely analýzy, vlastnosti materiálů a okrajové podmínky. Zejména u kompozitních materiálů s anizotropií je velmi obtížné získat materiálové vlastnosti. Pružné chování izotropních materiálů je charakterizováno čtyřmi vlastnostmi: Youngův modul, Poissonův poměr, modul ve smyku a objemový modul. Obecně se jako vstupní hodnoty používají Youngův modul a Poissonův poměr, které lze experimentálně snadno změřit, a měření smykového modulu není nutné. U anizotropních materiálů jsou však Youngův modul a modul ve smyku na sobě nezávislé a musí se měřit nezávisle.
Souběžně s výše popsaným úsilím o získání modulu pružnosti ve smyku pomocí zkoušek bylo provedeno mnoho studií, jejichž cílem bylo analyticky předpovědět vlastnosti materiálu.
Směšovací pravidlo (8), které je známé jako nejklasičtější metoda, umožňuje předpovídat vlastnosti materiálu pomocí jednoduchých výpočtů, které lze provádět ručně. Směšovací pravidlo však předpokládá, že vlákna a pryskyřice tvořící kompozit jsou zapojeny sériově nebo paralelně se směrem osy zatížení, nebo jinými slovy, pro snadný výpočet se předpokládají idealizované podmínky, takže je lze použít pouze pro velmi omezené kompozitní materiály, jako je jednosměrná výztuž. Metodu ekvivalentního začlenění navrženou Eshelbym (8) a její rozšíření, teorii Mori/Tanaka (9), lze aplikovat na více kompozitních materiálů než pravidlo míchání, ale její účinnost není dostatečně prokázána s výjimkou kompozitních materiálů s nespojitými vlákny, jako jsou vstřikované výrobky, protože teoretický vývoj vychází z předpokladu, že tvar začlenění je sféroid. Metoda homogenizace (10) použitá v tomto článku přitahuje pozornost jako metoda, která může tyto problémy řešit. Při homogenizační metodě se model, který reprezentuje mezoměřítkovou strukturu kompozitního materiálu (v případě GFRP velikost, při níž lze pozorovat heterogenní strukturu vláken a pryskyřice), použije k simulaci zkoušky materiálu pomocí metody konečných prvků a provede se numerická zkouška k vyhodnocení zdánlivé odezvy materiálu a k měření vlastností materiálu. Vzhledem k tomu, že interakci mezi vlákny lze důkladně zohlednit, lze výše uvedený problém řešit obecně pro jakýkoli kompozitní materiál.
V posledních letech je silná tendence aktivně využívat nové materiály za účelem zlepšení vlastností výrobků a na trh jsou postupně uváděny nové kompozitní materiály. Všestrannost metody homogenizace z ní činí nejvhodnější přístup pro trendy na trhu s tímto materiálem. Podrobnosti o metodě homogenizace naleznete ve stávajícím aplikačním sdělení č. 58 (11). Zde je důležité zdůraznit, že metoda homogenizace vyžaduje k provedení simulací také vstupní informace, jako je tvar mikrostruktury a materiálové vlastnosti jednotlivých vláken a pryskyřic. Jinými slovy, problém získání fyzikálních vlastností nelze vyřešit pouze technologií analýzy, ale vlastnosti kompozitních materiálů lze určit pouze kombinací měření a analýzy.
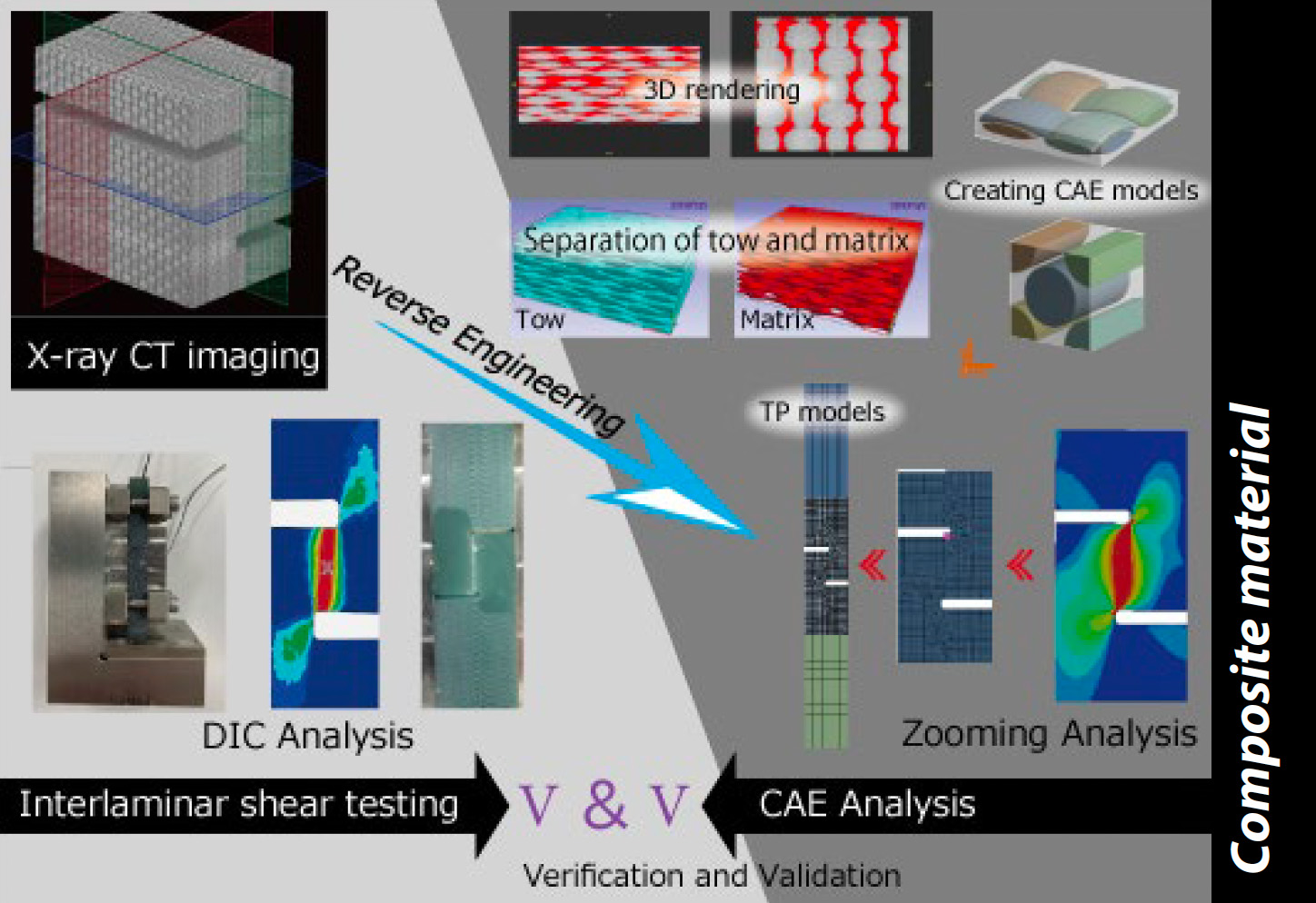
V aplikační poznámce č. 58 byly uvedeny příklady ověření jednoosých tahových vlastností kompozitních materiálů kombinací měření a analýzy. V tomto článku je pozornost zaměřena na režim smykové deformace a je představen příklad výzkumu, který kombinuje měření a analýzu. Nejprve byl vytvořen analytický model na základě výsledků pozorování heterogenní meziskalární struktury pomocí rentgenové počítačové tomografie (CT) a hodnoty vlastností byly předpovězeny provedením homogenizační analýzy. Platnost modelu byla ověřena porovnáním předpovězených výsledků se skutečnými výsledky pro čistý smyk. Kromě toho byla samostatně provedena analýza, při níž byly pomocí koeficientu tření reprodukovány omezující podmínky zkušebního vzorku vynucené zkušebním přípravkem použitým v experimentu (přípravek odpovídající normě JIS K 7092). Analytické výsledky byly porovnány s experimentálními výsledky, aby se ověřila platnost experimentálních výsledků.
Určení různých parametrů potřebných k vytvoření modelu
Hodnocení mezilamelových smykových vlastností GFRP tkaných materiálů
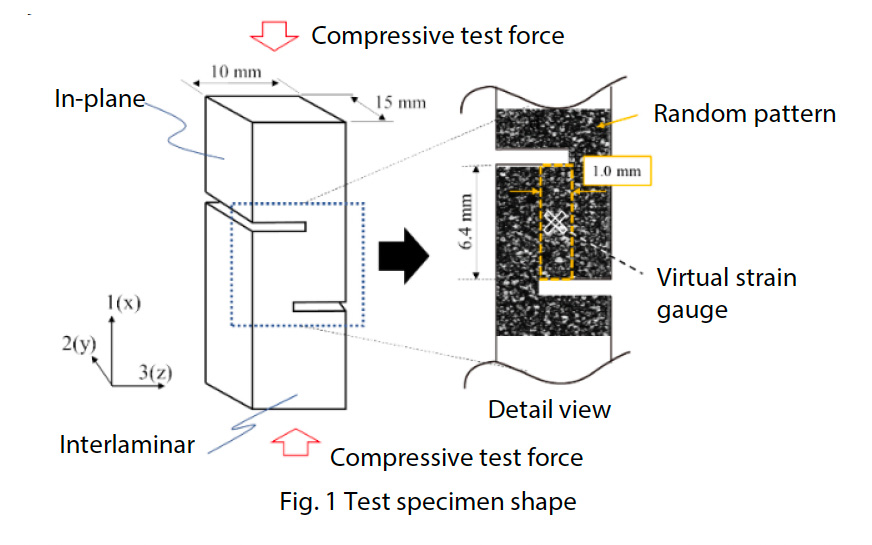
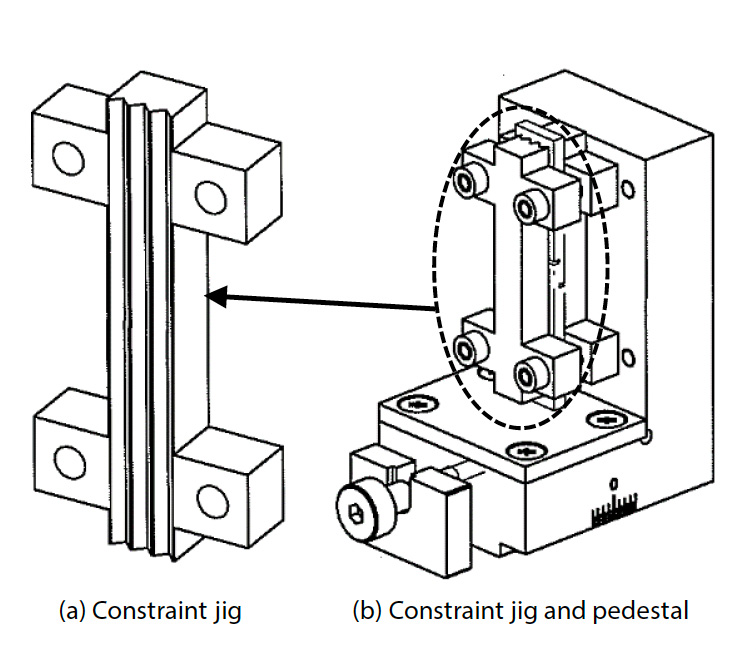
Jak je znázorněno na obr. 1, zkušební vzorek byl vyroben z hladké tkané ploché desky z GFRP o tloušťce přibližně 10 mm. Celková délka vzorku byla 80 mm a za účelem soustředění smykové deformace mezi vroubkované drážky vystavené smykovému zatížení byly vroubkované drážky překryty o 1 mm, aby se rozšířila oblast smykové deformace oproti tvaru uvedenému v JIS K 7092 (5), a rozložení deformace v oblasti smykové deformace bylo rovnoměrné (4). Šířka mezery mezi vrubovými drážkami byla navržena na 1 mm. Na povrch zkušebního vzorku byl nanesen náhodný vzor, a to tak, že byl aplikován černý sprej a následně bílý sprej. Vzorek byl zasazen do systému pro zkoušku mezilamelového smyku, který se skládal z přípravku vyhovujícího normě JIS K 7092 a přítlačné desky s mechanismem pro nastavení rovnoběžnosti. 
γXZ=|ε_ (+45) |+|ε_ (-45) | (1)
|ε_ (+45) | : Absolutní hodnota deformace získaná z výstupu virtuálního tenzometru instalovaného pod úhlem +45°.
|ε_ (-45) | : Absolutní hodnota deformace získaná z výstupu virtuálního tenzometru instalovaného pod úhlem -45°.
Jmenovité smykové napětí τXZ bylo vypočteno z rovnice (2).
τXZ= F/ab (2)
F: zkušební síla (N), a: vzdálenost mezi vroubkovanými drážkami (6,4 mm), b: šířka vzorku (15 mm).
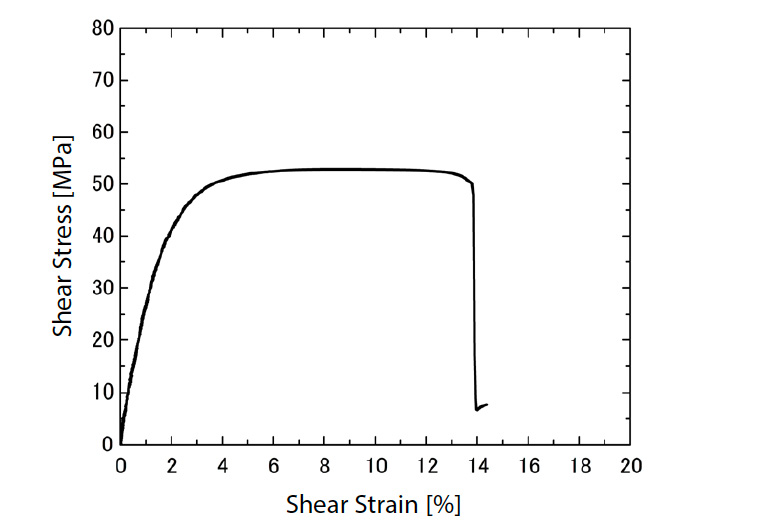
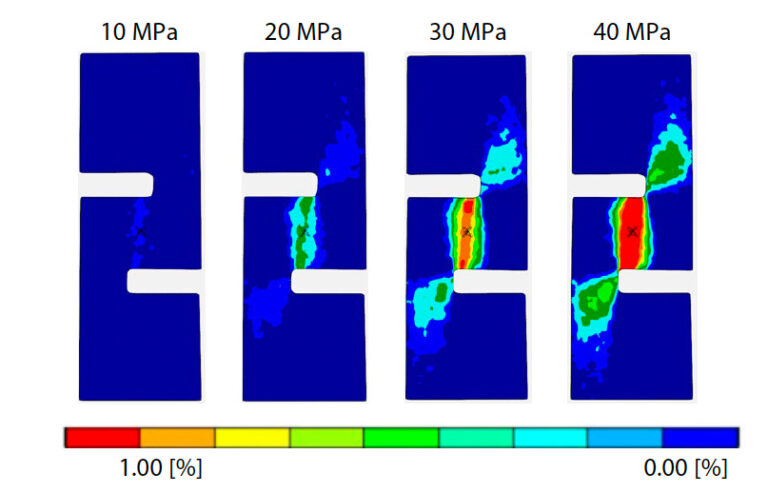
Na obr. 5 je znázorněn diagram mezilamelového napětí ve smyku a deformace hladkého tkaného GFRP získaný při této zkoušce. Závislost mezi napětím a deformací prostého tkaného GFRP je lineární až do smykového napětí přibližně 30 MPa, ale poté se stává nelineární a při přibližně 50 MPa se poddají. Jak bylo uvedeno výše, hladce tkaný materiál GFRP má strukturu, v níž je laminována tkanina ze skleněných vláken impregnovaná pryskyřicí. Proto je GFRP prostý tkaný materiál bohatý na pryskyřici v interlaminárním směru a má se za to, že nelinearita se objevila v důsledku tvárných vlastností pryskyřice. Na obr. 6 jsou znázorněny obrysové diagramy interlaminární smykové deformace z výsledků DIC analýzy při tlaku 10 až 40 MPa. Mezivrstevná smyková deformace je od začátku zkoušky rovnoměrně a široce rozložena mezi vruby prosté tkaniny z GFRP a tato tendence je stejná i při zvyšování zatížení působícího na zkušební vzorek. Ze závislosti s napětím v lineární počáteční oblasti, deformace 0,1 až 0,3 % na obr. 5, byl mezilaminární modul ve smyku vypočtený metodou nejmenších čtverců 2546,1 MPa.
Vyhodnocení omezujících podmínek vzorku měřením součinitele tření
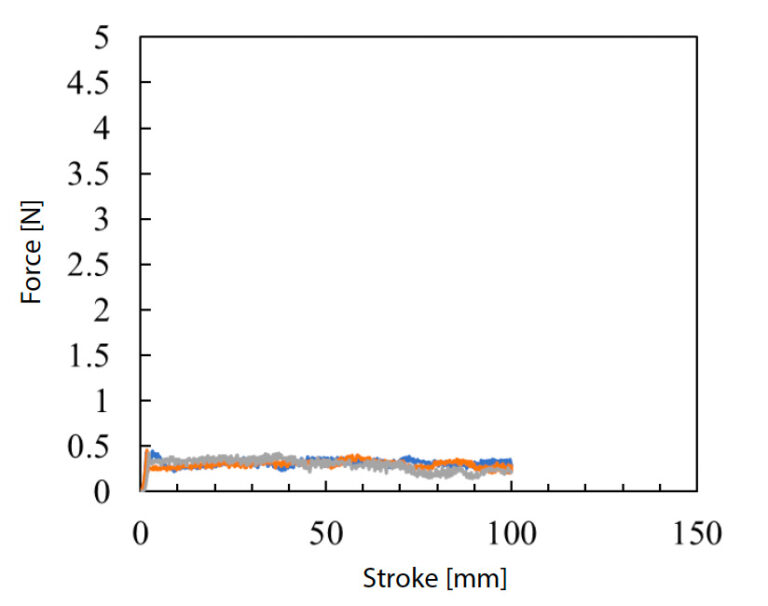
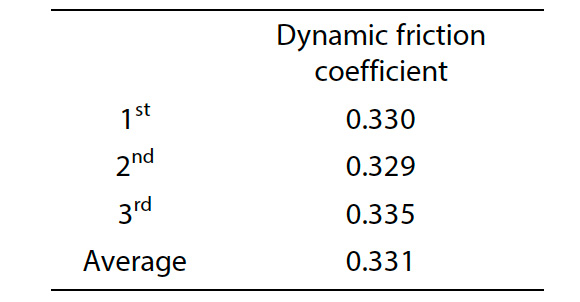
Omezující podmínky zkušebních vzorků použitých při zkoušce smykem v mezilamelovém směru byly odhadnuty měřením součinitele tření pomocí přesného univerzálního zkušebního stroje Autograph AGX-5NV a zařízení pro měření součinitele tření. Obr. 7 ukazuje průběh zkoušky. Při provádění zkoušky byla na zkušební prostor zkušebního stroje po vyříznutí vrubovaného vzorku umístěna plochá deska z hladce tkaného materiálu GFRP o tloušťce 10 mm a na plochou desku byl instalován omezovací přípravek tak, aby se jí dotýkala styčná plocha vzorku. Rychlost zkoušky byla nastavena na 100 mm/min a údaje o zkušební síle byly získány při zdvihu zkušebního stroje 100 mm. Pro potvrzení reprodukovatelnosti získaných údajů byly provedeny tři zkoušky. Koeficient dynamického tření pro použití v analýze CAE byl vypočten z průměrných údajů o zkušební síle pro zdvih 20 až 60 mm získaných při stabilní zkušební síle a hmotnosti přípravku. Na obr. 8 je znázorněn diagram závislosti zkušební síly na zdvihu a v tabulce 1 jsou uvedeny výsledky výpočtu součinitele dynamického tření. Z výše uvedených výsledků bylo zjištěno, že součinitel dynamického tření, který vzniká na styčné ploše mezi vzorkem a omezovacím přípravkem, je 0,33.
Získávání dat o tvaru vrubovaného vzorku pomocí rentgenového CT systému
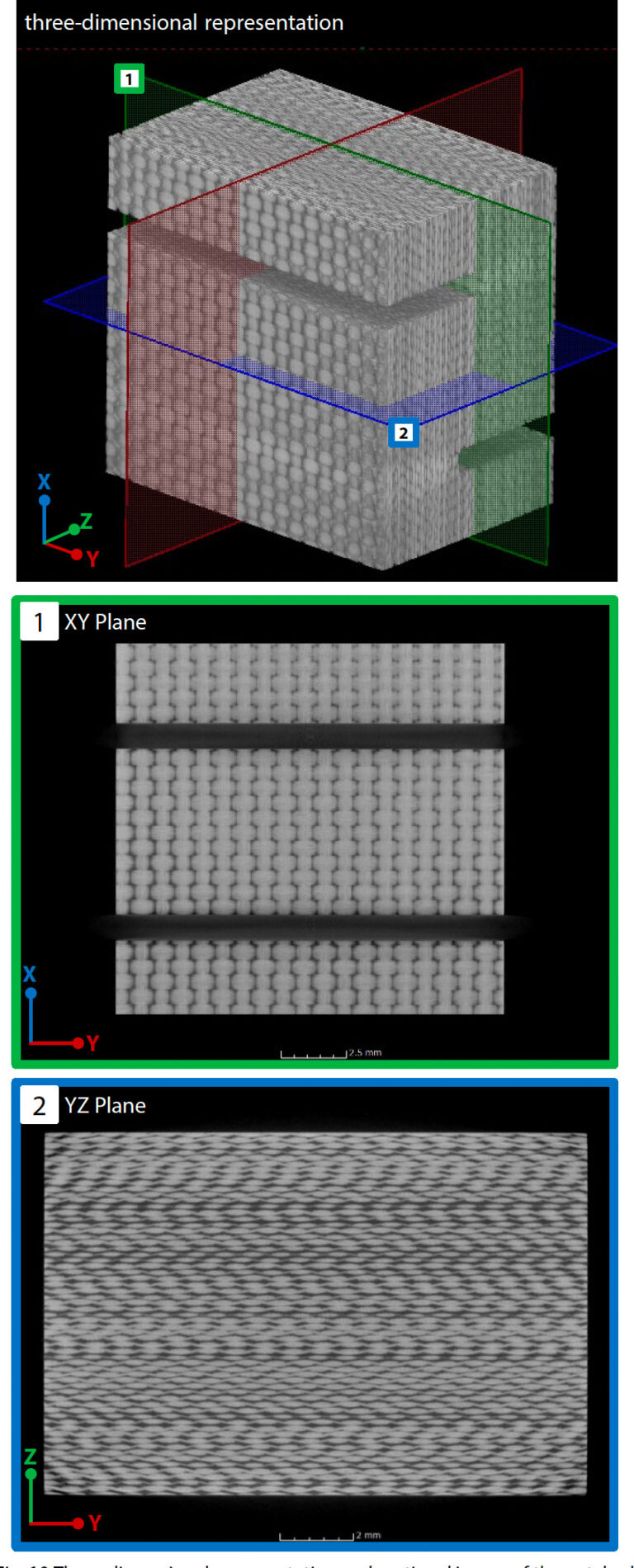
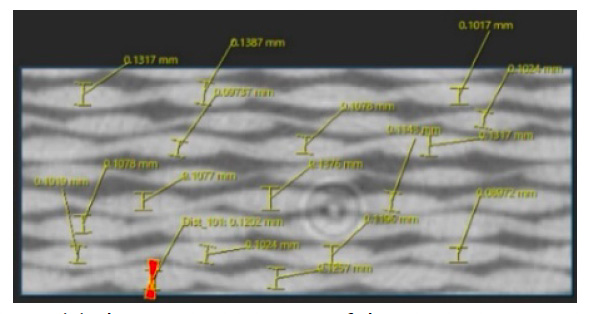
Pomocí mikroohniskového rentgenového CT systému inspXio™ SMX™-225 CT FPD HR Plus, který je znázorněn na obr. 9, byly získány snímky průřezu vzorku s vrubem pro určení tvaru analytického modelu. Za podmínek uvedených v tabulce 2 byly pořízeny CT snímky v blízkosti vrubové drážky zkoušky a několik set průřezových snímků bylo vyvedeno do formátu DICOM (Digital Imaging and Communications in Medicine). Na obr. 10 jsou zobrazeny snímky průřezů a trojrozměrné zobrazení vytvořené pomocí softwaru pro trojrozměrnou analýzu obrazu na základě snímků průřezů. Na snímku průřezu se oblasti s vysokou hustotou a vysokou absorpcí rentgenového záření zobrazují bíle a oblasti s nízkou hustotou a nízkou absorpcí rentgenového záření černě. Zpracování obrazu bylo provedeno za účelem vytvoření modelu ze snímku průřezu pro použití v analýze konečných prvků. Analýzou snímků průřezu získaných pomocí CT zobrazování pomocí softwaru Simpleware™ společnosti Synopsys byly identifikovány tvarové parametry mikrostruktury potřebné k vytvoření modelu pro analýzu. U analyzovaného materiálu GFRP s hladkou tkaninou jsou faktory, které ovlivňují vlastnosti materiálu, objemový obsah a tvar průřezu kabelu (svazek několika set až 1000 vláken uspořádaných v jednom směru) a vzdálenost mezi sousedními svazky vláken. Obsah jednovláknových vláken uvnitř vlečky má rovněž vliv na vlastnosti materiálu, ale v tomto analytickém snímku nebylo možné získat jasný kontrast ani v jemné oblasti uvnitř vlečky, takže byl určen porovnáním s výsledkem montáže. Podrobnosti jsou popsány níže v oddíle 3. Tyto tvarové parametry nejsou v celém materiálu rovnoměrné a jsou rozloženy s odchylkami. Proto byl v nástroji pro analýzu obrazu změřen poměrně široký rozsah zahrnující více svazků vláken a průměrná hodnota byla přijata jako tvar modelu analýzy.
Vytvoření modelu
Identifikace tvarových parametrů
Na obr. 11 je znázorněn objemový podíl vleku změřený pomocí softwaru Simpleware. Oblast vlečky a oblast matrice byly odděleny binarizací obrazu ve stupních šedi získaného z rentgenového CT pomocí vhodných prahů. Objemový podíl byl určen měřením objemu každé oddělené oblasti.
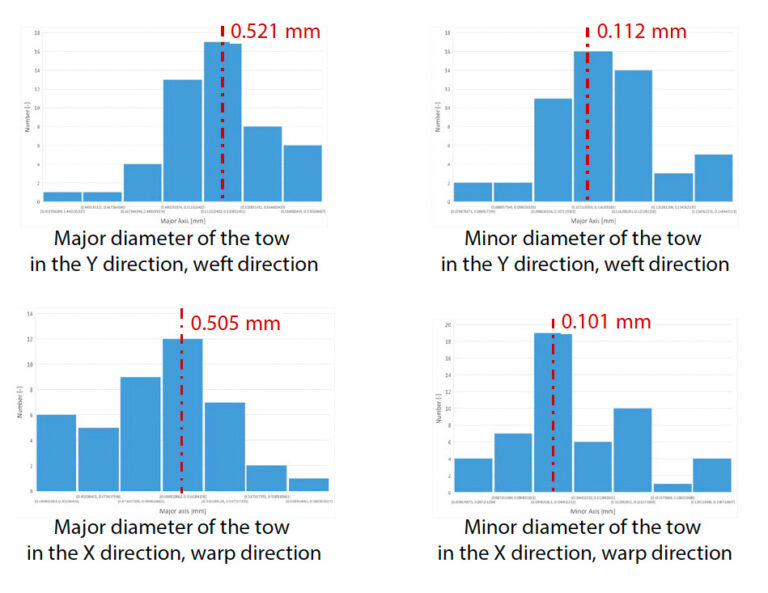
Obr. 12 ukazuje tvar příčného řezu vleku a naměřenou vzdálenost mezi vleky. Předpokládalo se, že vlek má eliptický průřez, a měřily se hlavní a vedlejší průměry. Náhodně bylo vybráno 49 vlečných sítí. Na obr. 12 je znázorněn výsledek vykreslení histogramu o 7 koších pomocí věty o odmocnině z počtu měřených bodů pro každý měřený parametr tvaru. Protože nebyla tendence, aby se všechny tvarové parametry jednoznačně shodovaly s obecnou statistickou funkcí, jako je Gaussovo rozdělení, byla jako tvarový parametr použita průměrná hodnota koše s nejvyšší pravděpodobností existence. Tento výsledek ukazuje, že tvar vleku ve směru X a Y se zřetelně liší. Obecně je však velmi vzácné navrhovat výrobek s ohledem na tyto směrově závislé mikrostruktury, proto byl tentokrát další průměr průměrných hodnot v obou směrech použit stejně pro tah v obou směrech.
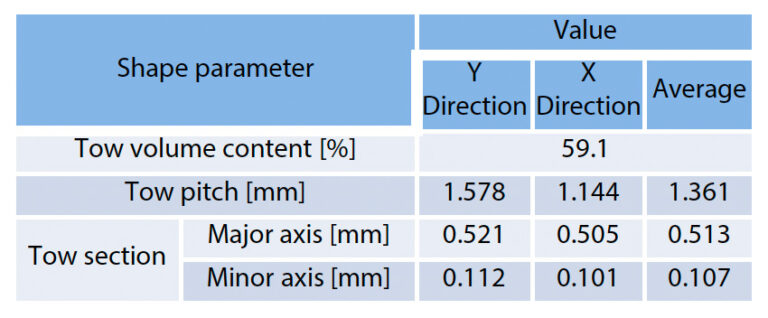
Na obr. 12 (c) je rovněž zobrazen obraz měření vzdálenosti mezi sousedními vleky. Tento tvarový parametr byl měřen z mimoplošného snímku. Hranice mezi oblastmi, které nejsou zakryty kolmým vlekem, a oblastmi, které jsou zakryty kolmým vlekem, jsou bohaté na plast, a proto se jeví tmavé. V důsledku toho se oblasti, které nejsou zakryty kolmým vlečením, a oblasti, které jsou zakryty kolmým vlečením, jeví jako samostatné obdélníkové útvary. Rozteč vlečných sítí byla definována jako vzdálenost mezi středovými body tohoto obdélníku. Stejně jako u tvaru příčného řezu vlečné sítě byla měřena vzdálenost mezi 49 vlečnými sítěmi. U rozteče mezi vleky byla pozorována tendence k závislosti na vertikálním a svislém směru vláken v bodě c) na stejném obrázku a poté byla do modelu analýzy použita průměrná hodnota. V tabulce 3 a na obr. 13 jsou shrnuty jednotlivé nakonec zjištěné tvarové parametry a skutečně vytvořené analytické modely pro numerický test.
Optimalizace tvarových parametrů
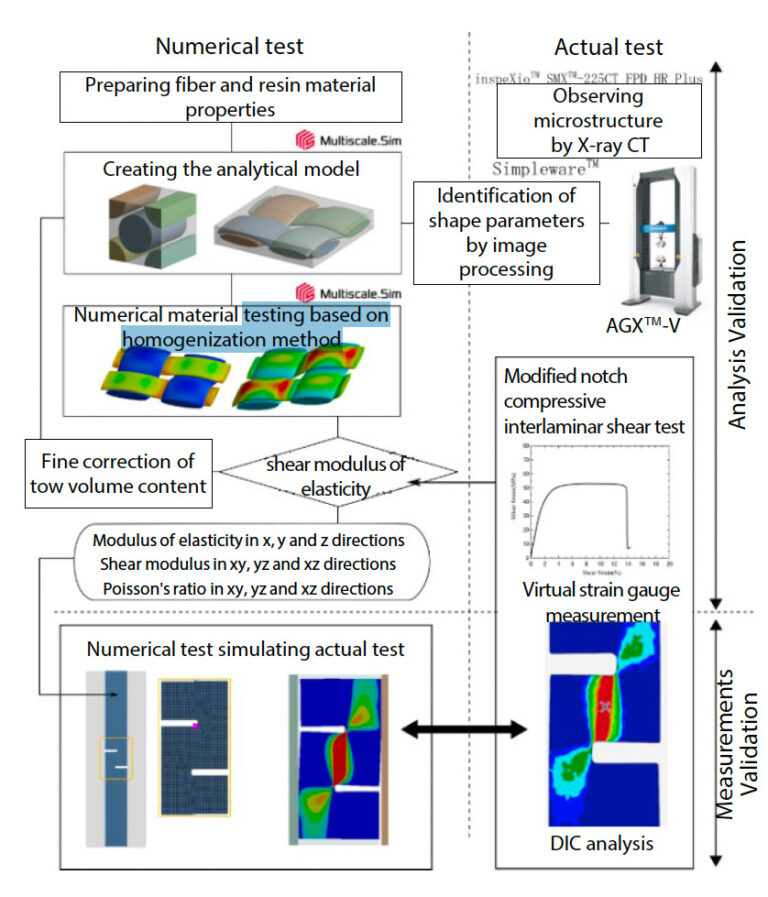
Materiály vyztužené spojitými vlákny, jako je například tkanina použitá v této analýze, mají tendenci vykazovat extrémně silnou anizotropii. Analytické metody založené na homogenizační metodě (10) jsou účinné pro analytické předpovědi vlastností materiálu, které charakterizují anizotropní chování. Metoda homogenizace poskytuje analytický přístup k vyhodnocení zdánlivé odezvy materiálu a v konečném důsledku k identifikaci vlastností materiálu provedením numerické zkoušky. test numerickým výpočtem pomocí modelu konečných prvků, který reprezentuje nehomogenitu mikrostruktury. Jednoduchým měřením materiálových vlastností jednotlivých vláken a pryskyřic (a vlastností materiálového rozhraní, pokud je třeba je zohlednit) nebo jejich získáním z databáze apod. lze získat anizotropní chování materiálu a materiálové vlastnosti pro všechny typy výztuže na základě jejich heterogenní mikrostruktury. Podrobnosti o této metodě analýzy jsou uvedeny v aplikační poznámce č. 58 (11). Celkový průběh analýzy je znázorněn na obr. 14. Byl učiněn pokus o ověření platnosti obou aspektů analýzy a měření. Analytická validace byla provedena pomocí výše popsané homogenizační analýzy. Požadovanou informací byl tvar mikrostruktury a vlastnosti materiálů, z nichž byla složena. Konkrétní hodnoty tvarových parametrů potřebných pro modelování mikrostruktury byly určeny použitím dat zjištěných pomocí rentgenového CT při zpracování obrazu, jak je popsáno v oddíle 2-3.
Validace zkušební metody
Pro ověření platnosti skutečné zkušební metody byla provedena analýza se stejným tvarem a okrajovými podmínkami jako při zkoušce. Materiálové vlastnosti materiálu hladké tkaniny použité v tomto modelu analýzy byly získány ve fázi ověřování analýzy. Porovnáním rozložení smykové deformace ve vzorku získaného analýzou s výsledkem naměřeným analýzou DIC bylo potvrzeno, že analytický výsledek dobře souhlasí se skutečným výsledkem zkoušky. Současně se analýza pokusila kvantifikovat podmínky ovlivňující výsledky zkoušky porovnáním koeficientu tření mezi přípravkem a vzorkem a analytických výsledků získaných prakticky změnou utahovacího zatížení přípravku.
Metoda analýzy
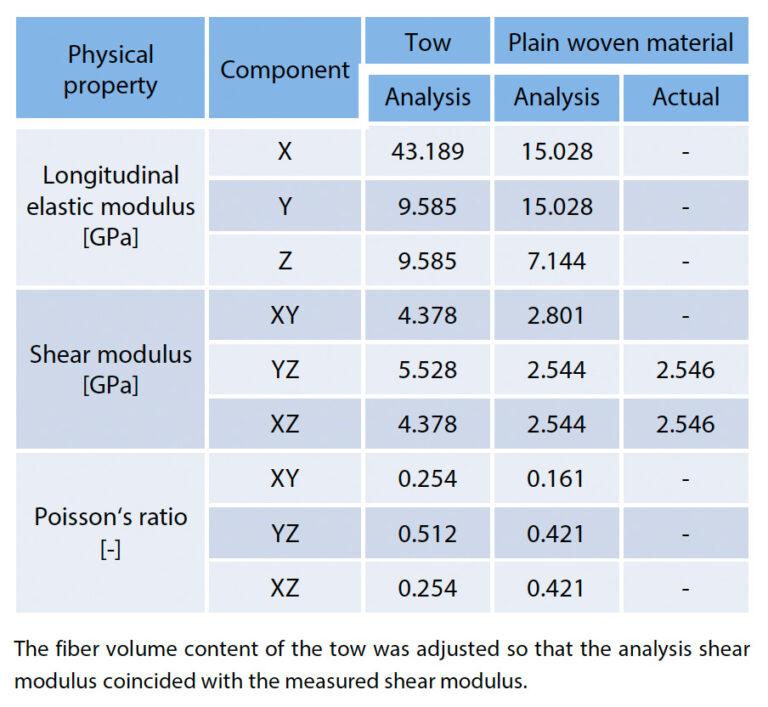
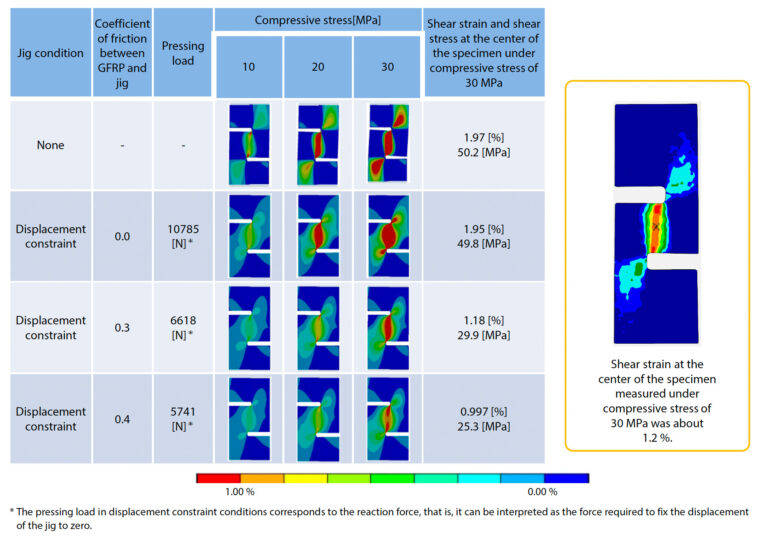
Nejprve byly pomocí homogenizační analýzy vypočteny ortotropní materiálové vlastnosti hladce tkaných materiálů GFRP. Na obr. 15 jsou znázorněny modely pevných těles a konečných prvků materiálu GFRP tkaniny použité při analýze. Jak bylo uvedeno výše, meziskalární tkané struktury byly identifikovány zpracováním obrazu z výsledků získaných pomocí rentgenového CT. Mezošupinový model předpokládá, že oblast vlečky je homogenní. Ve skutečnosti má materiál nehomogenní strukturu sestávající ze svazků vláken orientovaných v jednom směru, takže je nutné zajistit anizotropní vlastnosti materiálu, které správně odrážejí mikroskopickou strukturu. Proto je model znázorněný na obrázku (a-2) a obr. (b-2) byl připraven pro svazky vláken v oblasti vleku a pro získání fyzikálních vlastností byla provedena samostatná homogenizační analýza. Materiály, které tvoří kompozit, jsou sklo E (Youngův modul: 72,5 GPa, Poissonův poměr: 0,2) pro vlákna a epoxidová pryskyřice (Youngův modul: 3,5 GPa, Poissonův poměr: 0,35) pro pryskyřice. Předpokládalo se, že obě tyto vlastnosti jsou pružné, a odkazovalo se na hodnoty v databázi materiálů poskytnuté analytickým nástrojem. Při homogenizační analýze byly všechny materiálové vlastnosti charakterizující ortotropní vlastnosti materiálů z GFRP tkanin získány provedením numerických zkoušek simulujících ideální jednoosý tah a mezilamelový smyk pro tyto modely. Konkrétně se materiálové vlastnosti skládaly z 9 druhů fyzikálních vlastností: podélný modul pružnosti, Poissonův poměr a modul pružnosti ve smyku ve 3 směrech. Na obr. 16 je zobrazen analytický model provedený pro ověření experimentální strany. Model se skládal ze vzorku GFRP a omezovacího přípravku, který drží vzorek ve směru tloušťky. Tlaková zatížení a tlaková napětí na vzorcích a přípravcích byla definována přímo na plochách těchto dílů a ostatní geometrie (otvory pro šrouby přípravku, přípravek pro podepření vzorku z horní a dolní části obrázku atd. důsledně modelovány. Konkrétně byl spodní povrch vzorku na obr. 16 definován s omezením plného posunutí a horní povrch byl definován s tlakovým napětím 30 MPa. Při skutečné zkoušce bylo tlačné zatížení ve směru mimo rovinu aplikováno prostřednictvím momentu působícího na přípravek, ale v analýze byl posun přípravku omezen na nulu. Kromě toho byl analyzován i případ, kdy přípravek nebyl instalován. V blízkosti vrubu GFRP se očekávalo složité rozložení deformace, ale v oblasti dostatečně vzdálené od vrubu se očekávalo téměř rovnoměrné rozložení napětí a deformace. Proto byla část z GFRP rozdělena na oblast v blízkosti vrubu a ostatní oblasti a síť byla jemně nastavena pouze v blízkosti vrubu. Mezi dvěma díly s různou hrubostí sítě existovala nespojitá síť, ale realistický stav upevnění byl reprodukován definováním vícebodového omezení (MPC) na rozhraní. Z hlediska chování materiálu byly dílu z GFRP přiřazeny materiálové vlastnosti získané výše uvedenou homogenizační analýzou a předpokládalo se, že přípravek je tuhý a nedeformovatelný. Koeficient tření mezi hladce tkaným materiálem GFRP a přípravkem byl analyzován ve třech vzorcích, 0,0, 0,3 a 0,4, aby se potvrdil vliv na výsledky zkoušky. Z údajů o výsledcích analýzy, které zde byly získány, bylo zjištěno rozložení mezilamelové smykové deformace a hodnoty smykové deformace a smykového napětí ve středu vzorku. Platnost zkušebních podmínek byla ověřena porovnáním těchto výsledků s naměřeným rozložením smykové deformace získaným pomocí analýzy DIC a naměřenou smykovou deformací ve středu vzorku získanou pomocí virtuálního tenzometru. Při této zkoušce se v ideálním případě tlakové napětí 30 MPa působící na horní část vzorku přenáší stejně jako smykové napětí ve středu vzorku. Ve výsledcích analýzy bylo sledováno, zda bylo této ideální podmínky dosaženo.Výsledky analýzy CAE
Nejprve byla provedena homogenizační analýza na analytickém modelu znázorněném na obr. 16 a výsledky vyhodnocení ortotropních modulů pružnosti oblasti vlečky a celého hladce tkaného materiálu jsou uvedeny v tabulce 4. Vzhledem k tomu, že při zkoušce byla vyhodnocena smyková tuhost hladce tkaného materiálu, byl při analýze upraven objemový obsah vláken v oblasti vlečky tak, aby se analytický smykový modul shodoval s naměřeným smykovým modulem. Objemový obsah vláken v oblasti vlečky, který byl nakonec získán inverzním odhadem, činil přibližně 57,27 %. Tato hodnota se příliš nelišila od jiných studií provedených pomocí SEM a považuje se za přiměřenou. Tabulka 5 shrnuje výsledky jednotlivých případových studií, které využívaly optimalizovaný model pro změnu přítomnosti nebo nepřítomnosti omezovacího přípravku a změnu koeficientu tření mezi omezovacím přípravkem a vzorkem. Výsledky naměřeného rozložení smykové deformace z analýzy DIC jsou rovněž uvedeny vpravo a vně tabulky 5. Za všech podmínek je vidět, že smyková deformace je soustředěna poblíž středu vzorku umístěného mezi dvěma zářezy. Lze však usuzovat, že deformace vzorku je odlišná, protože rozložení deformace závisí na napěťových podmínkách v oblasti mírně vzdálené od středu a na okrajové straně obou vrubů. Pokud není přípravek instalován, je vidět, že existuje vysoká deformace stejného řádu jako ve středu vzorku, který se rozšiřuje od zářezu k okraji. To může být způsobeno deformací vzorku mimo rovinu. Výsledky také ukazují, že smykové napětí ve středu vzorku je větší než vnější tlak, což naznačuje, že nelze dosáhnout přesné deformace mimo rovinu smyku. Za podmínek, kdy je umístěn pevný přípravek, je oblast vysokého smykového napětí na koncové straně od vrubu malá, takže je vidět, že deformace vzpěru je potlačena. Potvrdilo se, že míra potlačení je výraznější s rostoucím součinitelem tření mezi prostým tkaným materiálem GFRP a přípravkem. Se zvýšením součinitele tření na 0,4 se však napětí ve středu vzorku stalo menším než vnější tlak. Předpokládá se, že je to způsobeno tím, že energie vnějšího tlaku se ztrácí v důsledku odporové třecí síly v míře, kterou nelze ignorovat. Při skutečné zkoušce nelze součinitel tření kontrolovat, a proto je nutné použít vhodné tlakové zatížení, aby nebyla příliš potlačena deformace v rovinném směru a zároveň potlačeno vybočení vzorku mimo rovinu.
Při zkoušce popsané v části 2-2 se potvrdilo, že koeficient tření mezi materiály je přibližně 0,3. Za těchto podmínek je smykové napětí ve středu vzorku rovno vnějšímu tlaku, což znamená, že je dosaženo ideálních smykových podmínek.
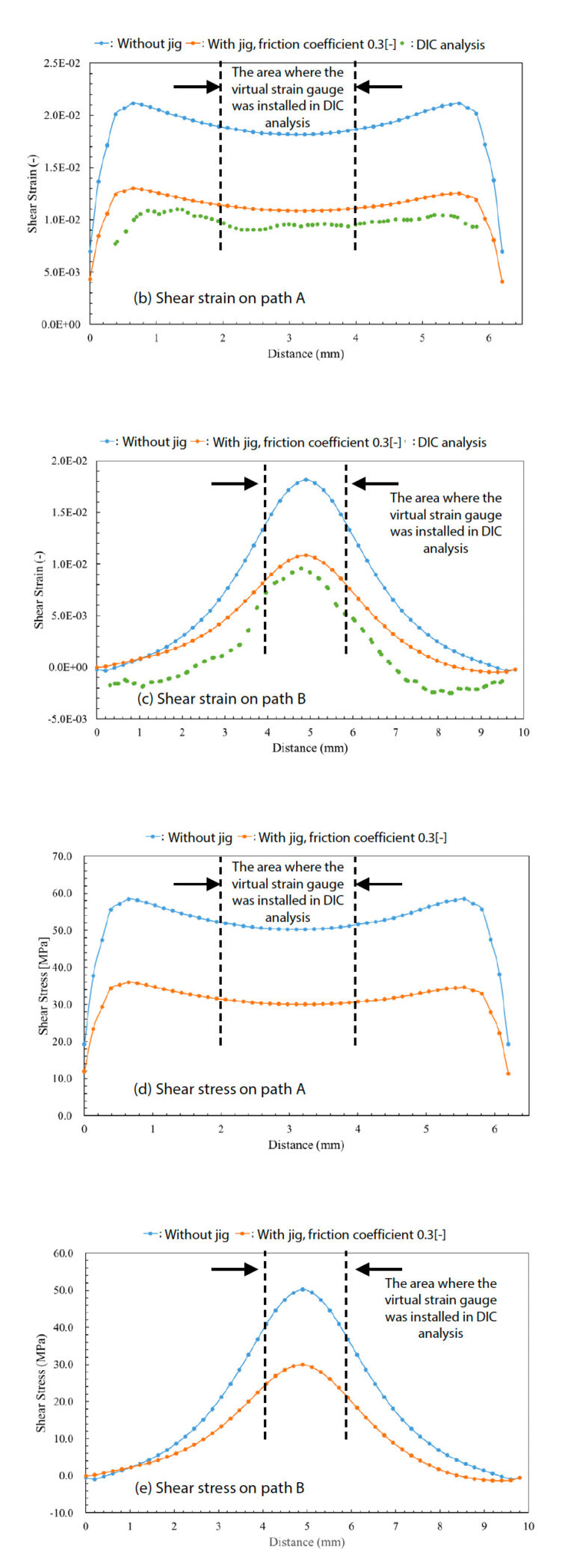
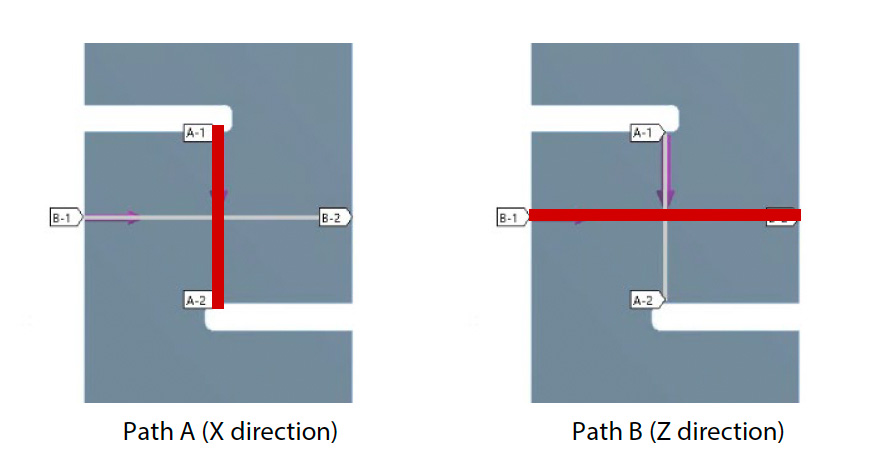
Nakonec, abychom si podrobněji prohlédli rozložení smykové deformace v blízkosti zářezů, byly výsledky smykové deformace a smykového napětí vyneseny do grafu nad dvěma dráhami znázorněnými na obr. 17 (a). Výsledky jsou uvedeny na obr. b) až e). Střed vzorku odpovídá vzdálenosti 3,2 mm v dráze A a 5,0 mm v dráze B. V analýze DIC se oblast, kde byl instalován virtuální tenzometr, nachází blízko středu. Pro přesnou zkoušku mezivrstvového smyku se očekává, že se střední část vzorku nachází v ideálním smykovém režimu, ale je také žádoucí, aby podobné podmínky existovaly v širokém okolí. Zejména při měření lokálních hodnot deformace tenzometrem je žádoucí udržovat konstantní hodnotu v oblasti měření přibližně 2 x 2 mm.
Ve stavu, kdy je umístěn omezovací přípravek, jak je znázorněno na obr. 17 (b) a (c), je toho téměř dosaženo a očekává se, že mezilamelové smykové charakteristiky vzorku lze měřit s určitou přesností. Na druhou stranu v případě, že přípravek není umístěn, je v důsledku vybočení mimo rovinu střední smyková deformace abnormálně velká ve srovnání s měřením a výsledek na dráze A je pozorován jako pozoruhodně konvexní směrem dolů, jak je znázorněno na obr. 17 (b).
Bylo také zkontrolováno rozložení smykového napětí a bylo zjištěno, že za podmínek, kdy byl umístěn omezující přípravek, bylo smykové napětí znázorněné na obr. 17 (d) do určité míry široce rozloženo na dráze A podobně jako smyková deformace. Kromě toho bylo potvrzeno, že virtuální tenzometr použitý v analýze DIC byl široce rozložen v oblasti, kde byl virtuální tenzometr instalován na dráze B, která se nacházela poblíž středu mezi vrubovými drážkami odpovídajícími vzdálenosti 2 až 4 mm na dráze B. Při zkoušce neexistuje jiná metoda vyhodnocení napětí než výpočet jmenovitého smykového napětí vydělením zkušební síly naměřené v siloměru zkušebního stroje plochou průřezu vzorku, jak je uvedeno v rovnici (2) v oddíle 2-1. Ve výsledcích uvedených na obr. 17(d) nedochází v blízkosti vrubu ve vzorku ke koncentraci napětí a rovnoměrné rozložení napětí v intervalu mezi vruby 6,4 mm lze ověřit pouze analýzou CAE. Výsledky analýzy CAE neprokázaly žádnou významnou lokální koncentraci napětí, což je důkazem, že zkušební metody a zkušební geometrie použité při zkoušce jsou užitečné pro vyhodnocení jmenovitého smykového napětí i lineární a nelineární deformace.
Tyto výsledky naznačují, že zkoušku mezilamelového smyku lze reprodukovat umístěním přípravku ve směru mimo rovinu vzorku a jeho podepřením mírným zatížením, které nenarušuje tangenciální skluz materiálového rozhraní nástroj - vzorek, ale potlačuje normálové vzpěr.
Souhrn
V tomto příspěvku jsme představili případ, kdy byly vyhodnoceny mezilamelové smykové charakteristiky hladce tkaných materiálů GFRP metodou mezilamelové smykové zkoušky s využitím modifikované metody vrubové komprese, a to jak na základě experimentální analýzy DIC, tak analýzy CAE.
Analytický model CAE byl sestaven na základě nastavení okrajových podmínek mezi vzorkem a omezovacím přípravkem s ohledem na koeficient tření. Bylo zjištěno, že výsledky analýzy DIC a analýzy CAE jsou téměř shodné v následujících třech bodech získaných mezi vrubovými drážkami vzorku.
1. Obrysový diagram rozložení smykové deformace
2. Tvar rozložení smykové deformace ve směru X
3. Tvar rozložení smykové deformace ve směru Z
Kromě toho bylo rozložení napětí mezi vrubovými drážkami vypočtené analýzou CAE široké a rovnoměrné a nebyla pozorována žádná lokální koncentrace napětí.
Metoda zkoušení ve smyku v mezilaminárním směru s modifikovaným vrubovým stlačením použitá při vlastní zkoušce se ukázala jako užitečná nejen pro získání lineární a nelineární deformace, ale také pro vyhodnocení jmenovitého smykového napětí.
Odkazy
1) Pettersson KB, Neumeister JM. Tahová souprava pro kompozitní smykovou zkoušku IDNS. Compos Part A Appl Sci Manuf 2006; 37 (2) : 229-42.2) Melin LN, Neumeister JM. Měření konstitutivního smykového chování ortotropních kompozitů a vyhodnocení modifikovaného Iosipescuova testu. Compos Struct 2006; 76 (1-2): 106-15.
3) Julio F. Davalos a, Pizhong Qiao b, Vinod Ramayanam a, Luyang Shan b, Justin Robinso. Torze voštinových sendvičových nosníků z FRP se sinusovou konfigurací jádra. Compos Struct 2009; 88: 97-111.
4) T.Murakami, T.Matsuo, T.Sumiyama, Experimental method and evaluation for interlaminar shear properties of randomly oriented strand thermoplastic composites based on modified double-notch specimen and two dimensional digital image correlation. J. Compos. Mater., v tisku, https://doi.org/10.1177/0021998320967719 (2020).
5) JIS K 7092. Zkušební metoda pro stanovení mezivrstevní pevnosti ve smyku plastů vyztužených uhlíkovými vlákny pomocí vzorku s dvojitým zářezem. In: JIS handbook. Tokyo: Japanese Standard Association; 2010.
6) Bouette B, Cazeneuve C a Oytana C. Effect of strain rate on interlaminar shear properties of carbon/epoxy composites. Compos Sci Technol 1992; 45: 313-321.
7) Internetové stránky Ministerstva hospodářství, obchodu a průmyslu: https://www.meti.go.jp/policy/digital_transformation/index.html.
8) J.D.Eshelby, The determination of the elastic field of an ellipsoidal inclusion and related problems, Proc. Roy. Soc. Lond, svazek A241, str. 376- 396 (1957).
9) T. Mori, K. Tanaka, verage stress in matrix and average elastic energy of materials with misfitting inclusions, Acta Metallurgica, Vol.21, No.5, pp.571- 574 (1973).
10) Terada, K., Kato, J., Hirayama, N., Inugai, T. a Yamamoto, K., A method of two-scale analysis with micromacro decoupling scheme: application to hyperelastic composite materials, Computational Mechanics, Vol.52, pp.1199-1219 (2013).
11) Koji Yamamoto, Takashi Murakami, Satoshi Iguchi, Zen Miyazaki Aplikační poznámka č. 58 Verifikace a validace (V&V) výsledků simulace jednoosé tahové zkoušky kompozitních materiálů: Fúze skutečného měření a homogenizační analýzy https://www.shimadzu.com/an/sites/shimadzu.com.an/files/pim/pim_d ocument_file/applications/application_note/11055/jpi320003.pdf
12) https://www.cybernet.co.jp/ansys/product/lineup/multiscale/multiscale/
13) https://www.cybernet.co.jp/ansys/product/
Stáhnout
- Aaplikace: Ověření použitelnosti modifikované metody zkoušení vrubového tlaku v mezilamelovém smyku
English 
German 
Czech 
Slovak 
Bulgarian 
Romanian 